Actividad 9. Alta tensión. Simplificación de fracciones
Escucha el siguiente audio.
Unidad 2. Actividad 9. Alta tensión
Propósito:
El propósito de esta actividad es que aprendas a simplificar fracciones.
¿Te has preguntado cuántas equivalencias pueden tener una fracción? De todas esas equivalencias, ¿cuál será la más simple? Coméntalo con tus compañeros, tu asesor o con otras personas.
Para hacer instalaciones eléctricas o para repararlas, los electricistas utilizan cables de diferente grosor. En esa labor, es muy útil saber simplificar fracciones.
Ejercicio 1
Escucha con atención:
Rafael y Felipe son electricistas. Necesitan reemplazar un cable. Usaron un calibrador para determinar que el diámetro del cable corresponde a las siguientes medidas en pulgadas:
, 
, 
,
, 
y 
Con base en la información anterior, contesta las siguientes preguntas:
a. ¿Son equivalentes todas las medidas que tomaron Rafael y Felipe?
b. De las diferentes opciones, ¿con cuál crees que se comercialice el cable que necesitan? Explica tu respuesta:
De las seis fracciones, la que utiliza las unidades fraccionarias más grandes es . Esta es también la fracción cuyo denominador tiene el número más pequeño.
En un conjunto de fracciones equivalentes, la que tiene el número más pequeño en el denominador recibe el nombre de “fracción en su mínima expresión”.
Ejercicio 2
En las siguientes fracciones equivalentes, anota cuál de ellas ha sido reducida a su mínima expresión. Usa como apoyo los materiales de tu caja de matemáticas.
a. 
.
b. 
.
c. 
.
d. 
.
Escucha el siguiente audio.
Audio (insertar pista 32 del LA en audio FyP)
Una forma de simplificar una fracción es mediante la factorización.
•
La factorización implica descomponer un número en sus factores primos.
Por ejemplo, los factores primos del 12 son: 2 y 3, porque son números primos que, al multiplicarse, dan 12 como resultado. Escucha:
2 × 2 × 3 = 12
Para simplificar una fracción utilizando la factorización, hay que comenzar por descomponer el numerador y el denominador en factores primos.
Por ejemplo, la factorización de la fracción 24 setentaidosavos comienza con la descomposición de 24 y 72 en factores primos:
24 2 × 2 × 2 × 3
72 2 × 2 × 2 × 2 × 3 × 3
Los factores que son comunes al numerador y al denominador se eliminan uno a uno:
Los factores no eliminados se convierten en el numerador y denominador de la fracción. Cuando se eliminan todos los factores, entonces el número que queda es 1. Así:
24 1
72 3
Ejercicio 3
Como ya escuchaste, la factorización de la fracción 
comienza con la descomposición de 24 y 72 en factores primos:
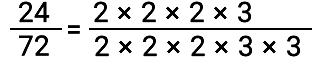
Recuerda que los factores primos comunes al numerador y al denominador se eliminan uno a uno:
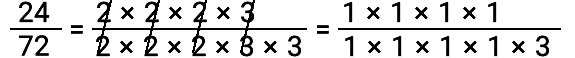
Los factores primos no eliminados se convierten en el numerador y denominador de la fracción. Cuando se eliminan todos los factores, entonces el número que queda es uno. Como en el procedimiento anterior, donde por la eliminación de los números dos y tres del numerador nos dio uno.
Entonces, la fracción resultante es uno sobre tres, es decir, un tercio.
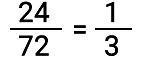
Ejercicio 4
Con base en la información anterior, factoriza las siguientes fracciones apoyándote en la caja de matemáticas del módulo.
a.
b.
c.
Presiona aquí para continuar