Unidad 4. Actividad 17. Tradiciones ancestrales

Propósito:

  • Resolverá probelmas de conteo a partir de elaborar listas y diagramas de árbol.

    • Escucha el audio que aparece a continuación.

    A continuación encontrarás los botones Ejecutar y Pausa para escuchar o pausar el siguiente audio. Avanza con Tabulador o retrocede con Shift+Tabulador.

    Audio (insertar pista 48 del LA en audio IyG)
    Actividad 17
    Tradiciones ancestrales
    El propósito de esta actividad es que resuelvas problemas de conteo a partir de elaborar listas y diagramas de árbol.

    ¿Consideras los tés remedios que curan algunos males o enfermedades? ¿Sabes cómo prepararlos y los riesgos que puede tener una mala combinación? Coméntalo con tu asesor o asesora.

    Se sabe que en México existe una medicina basada en el conocimiento de las propiedades curativas de las hierbas. Lo que no se sabe es que el uso inadecuado de las plantas puede traer consecuencias graves.

    Paquita nació con ictericia, es decir, con la piel de color amarillo.

    Su hermana Lola pensó prepararle un té, como lo hacía la abuela, haciendo combinaciones con estas hierbas que dejó la abuela: menta, ajenjo, prodigiosa, hierbabuena, epazote y alfalfa.

    Unidad 4. Actividad 17. Ejercicio 1

    a. ¿Cuántos tés de tres hierbas diferentes se pueden hacer con las hierbas que la abuela le dejó a Lola?


    b. Lola sabe que necesita combinar tres hierbas, pero no recuerda cuáles. ¿Qué probabilidad tiene Lola de preparar el té correcto?


    c. Compara sus repuestas con las de sus compañeros. ¿Qué consejo le daría a Lola?


    Si tuviste alguna dificultad para contestar las preguntas anteriores, analiza el procedimiento que llevó a cabo doña Juana ante una situación similar.

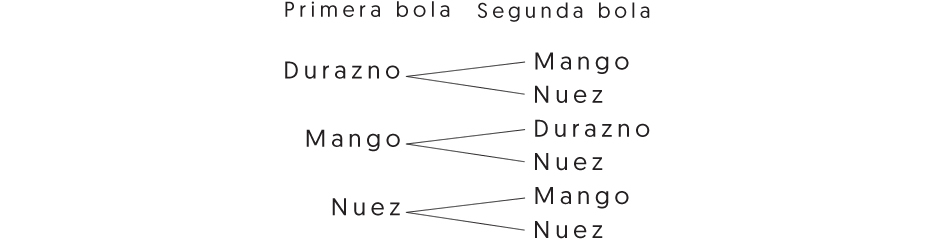
    Doña Juana vende helados de tres sabores: durazno, mango y nuez. ¿Cuántas combinaciones puede hacer si sirve dos bolas en cada vaso?

    Con el apoyo de una persona normovisual, elabora el siguiente diagrama. Se pueden utilizar diferentes materiales para generar el contorno del mismo como: silicón, foami, palitos, cartulina o estambre. Examínala para que conozcas el diagrama de árbol en donde se representan las opciones que tiene doña Juana.

     

    Imagen del gráfico que debes elaborar con ayuda de una persona normovisual

    Se puede imprimir la imagen anterior a mayor tamaño presionando el siguiente botón (sirve como plantilla): Imprimir


    Doña Juana usa ese diagrama de árbol para que sus clientes decidan cómo quieren su helado. Se pueden hacer seis combinaciones diferentes si se toma en cuenta la forma de acomodar los sabores; es decir, si se toma como diferente el helado de durazno con mango al de mango con durazno, el helado de durazno con nuez al de nuez con durazno y el helado de mango con nuez al de nuez con mango.

    El diagrama de árbol es un recurso que permite ordenar todas las posibles combinaciones y contarlas.

    Unidad 4. Actividad 17. Ejercicio 2

    En el comedor de la escuela hay un anuncio como el siguiente:

    Menú de hoy
    Sopa de fideo o consomé
    Arroz o espagueti
    Guisados: pollo con mole, bistec de res en salsa verde o chiles rellenos
    Postre gelatina de fresa

    En el siguiente espacio, describe las combinaciones que se pueden realizar con el menú.


    Responde.

    a. Si llegan 15 personas al comedor, ¿todas pueden pedir una combinación de alimentos diferentes? ¿Por qué?


    b. La encargada del comedor piensa meter dos postres a elegir. ¿Cuántas combinaciones de alimentos podrían hacerse?


    c. Además de los dos postres, ella quiere agregar ensalada en el segundo tiempo. ¿Cuántas combinaciones de alimentos podrán hacerse?


    Unidad 4. Actividad 17. Ejercicio 3

    Contesta.

    a. ¿Cuántos números diferentes puede escribir con los dígitos 1 y 2, si solo los empleas una vez en cada número?


    b. ¿Cuántos números diferentes se pueden escribir con los dígitos 1, 2 y 3 si solo los empleas una vez en cada número?


    c. ¿Cuántos números de dos cifras puedes formar con los dígitos 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9?


    d. A una reunión llegaron 10 personas; todas se saludaron entre sí. ¿Cuántos saludos hubo en total?


    e. Rocío tiene 6 blusas y 8 faldas; sin considerar que las combinaciones sean de su agrado, ¿cuántas son las formas en que puede combinarlas?


    Escucha el audio que aparece a continuación.

    A continuación encontrarás los botones Ejecutar y Pausa para escuchar o pausar el siguiente audio. Avanza con Tabulador o retrocede con Shift+Tabulador.

    Audio (insertar pista 49 del LA en audio IyG)
    Al resolver problemas que exigen conteo, es posible usar un diagrama de árbol.

    También se puede calcular mediante multiplicaciones.

    En el caso de que se quiera combinar una lista de datos, se multiplica
    n x (n -1) x (n – 1 - 1), donde n es el número de datos.

     

    Presiona aquí para continuar