Unidad 2. Actividad 9. Viaje a una historia lejana
Propósito:
Escucha el audio que aparece a continuación.
Audio (insertar pista 27 del LA en audio IyG)
¿Sabías que los egipcios desarrollaron sus conocimientos geométricos debido, entre otras cosas, a las constantes inundaciones que ocasionaba el río Nilo?
Generalmente los historiadores intentan reconstruir los hechos importantes que ocurrieron en el pasado, y explicar por qué y cómo ocurrió. Ellos realizan constantes “viajes al pasado”, donde las matemáticas cumplen un papel importantísimo al tratar de ubicar en tiempo y espacio cada suceso.
Para tener una idea clara de cómo eran los complejos funerarios, los alumnos de la Escuela Nacional de Antropología e Historia van a construir una maqueta a escala con aserrín aglomerado. Reconstruirán los tres complejos funerarios de Abusir: el de Neferirkara, Neuserray Sahura.
Realiza el Ejercicio 1 de la Actividad 9 en la Unidad 2, que aparece enseguida.
Unidad 2. Actividad 9. Ejercicio 1
La pirámide de Neferirkara tendrá una altura de 14 centímetros y una base cuadrada cuyo lado medirá 21 centímetros; irá montada en un prisma cuadrangular que medirá 23 centímetros de lado y 2 centímetros de altura. ¿Cuántos centímetros cúbicos de aglomerado necesitarán los alumnos para construirla?
Para calcular el volumen del prisma.
a. ¿Cuál es la fórmula para calcular el volumen de un prisma? (celda para fórmula)
b. ¿Cómo es la forma de la base del prisma donde irá montada la pirámide?
¿Cuál es su área?
c. ¿Cuánto medirá la altura del prisma?
d. ¿Cuál será el volumen del prisma?
Para calcular el volumen de la pirámide.
e. ¿Cuál es la fórmula para calcular el volumen de una pirámide?
f. ¿Cómo es la forma de la base de la pirámide?
¿Cuál es su área?
g. ¿Cuánto medirá la altura de la pirámide?
h. ¿Cuál será el volumen de la pirámide?
i. ¿Cuántos centímetros cúbicos de aglomerado se requieren para construir en la maqueta una de las caras del complejo funerario Neferirkara, la cual tiene 21 centímetros de ancho y 14 centímetros de alto y tiene que servir de base del complejo de esa cara de 23 centímetros y 2 centímetros de alto?
Escucha el audio que aparece a continuación.
Audio (insertar pista 28 del LA en audio IyG)
La fórmula para calcular el volumen de un prisma es área de la base por la altura.
Resuelve los ejercicios 2 y 3 de la Actividad 9, que aparecen enseguida.
Unidad 2. Actividad 9. Ejercicio 2
Recuerda que la fórmula para calcular el volumen de un prisma es: ![]() . Para hacer los cálculos, pide el apoyo de tu asesor.
. Para hacer los cálculos, pide el apoyo de tu asesor.
Resolvamos otros problemas
Renato vive en Jalisco. Está interesado en comerciar carritos de madera. Para ello, visitó una cooperativa en el estado de Chiapas, en la que se producen carritos con las siguientes características:
- Llantas de 5 centímetros de diámetro por 2 centímetros de ancho
- Cabina de 12 centímetros de ancho por 12 centímetros de alto y 12 centímetros de profundidad
- Caja de 12 centímetros de alto por 12 centímetros de ancho y 30 centímetros de profundidad
- Llantas de 3 centímetros de diámetro por 2 centímetros de ancho
- Cabina de 10 centímetros de ancho por 10 centímetros de alto y 10 centímetros de profundidad
- Caja de 12 centímetros de alto por 10 centímetros de ancho y 40 centímetros de profundidad
- Llantas de 4 centímetros de diámetro por 2 centímetros de ancho
- Cabina de 12 centímetros de ancho por 12 centímetros de alto y 12 centímetros de profundidad
- Caja de 15 centímetros de alto por 15 centímetros de ancho y 15 centímetros de profundidad
Un miembro de la cooperativa le explicó a Renato que el precio de los carritos está determinado por la cantidad de decímetros cúbicos de madera que lleva su elaboración.
a. ¿Cuál de los tres carritos tiene mayor costo?
b. ¿Cuál tiene menor costo?
c. ¿Cómo lo supiste?
Unidad 2. Actividad 9. Ejercicio 3
En el centro del pueblo van a poner una fuente que tiene las siguientes dimensiones:
- Un cilindro de 3 metros de diámetro por 6 metros de altura
- Un remate superior con forma de paralelepípedo de 5 metros por 5 metros y 0.5 metros de ancho
Contesta las siguientes preguntas.:
a. ¿Cuántos metros cúbicos de concreto se necesitan para hacer la base cilíndrica de la fuente?
b. ¿Cuántos metros cúbicos de concreto se necesitan para hacer la parte de arriba de la fuente?
c. Para sostener la fuente, el ingeniero va a poner cimientos en forma de cilindro cuya base mide 10 metros de diámetro y tiene una altura 3 metros. ¿Cuántos metros cúbicos de material necesita para poner los cimientos?
d. En total, ¿cuántos metros cúbicos de material se requieren para hacer la fuente?
Recuerda que la fórmula para calcular el área de la base del cilindro es ![]()
Escucha el audio que aparece a continuación.
Realiza el Ejercicio 4 de la Actividad 9, que aparece enseguida.
Audio (insertar pista 29 del LA en audio IyG)
Locutor:
Pista 29
Si tuviste alguna dificultad para calcular el volumen del cilindro, te servirá mucho escuchar cómo lo hizo Cristina.
Primero, calculó el área de la base con la fórmula pi por radio al cuadrado.
El radio es la mitad del diámetro: 1.5, en este caso.
El área es igual a 3.14 x 2.25 = 7.065; 7.065 metros cuadrados.
Después, Cristina calculó el volumen del cilindro con la fórmula: volumen es igual a área de la base por la altura o Ab x h.
Por tanto, el volumen del cilindro es igual a 7.065 x 8 = 56.52; 56.52 metros cúbicos, aproximadamente.
Unidad 2. Actividad 9. Ejercicio 4
Demetrio fabrica muebles rústicos de madera. Él hace mesas con las siguientes medidas:
- Base rectangular de 50 centímetros por 60 centímetros
- Altura de 90 centímetros
- Superficie circular de 150 centímetros de diámetro y 8 centímetros de ancho
a. ¿Cuántos centímetros cúbicos de madera lleva cada mesa?
b. ¿A cuántos decímetros cúbicos equivalen?
c. Demetrio necesita transportar 7 mesas. Aproximadamente, ¿cuánto pesará la carga si cada decímetro cúbico pesa 0.3 kilogramos?
Ten presentes las fórmulas para calcular el volumen de prismas.
- Prisma:
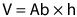 (área de la base por la altura)
(área de la base por la altura)
- Cilindro:
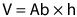 (área de la base por la altura), donde
(área de la base por la altura), donde 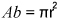
- Pirámide:
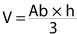 (Área de la base por la altura entre 3)
(Área de la base por la altura entre 3)
Escucha el audio que aparece a continuación.
Audio (insertar pista 30 del LA en audio IyG)
Para calcular el volumen de una figura compuesta por varios cuerpos geométricos, puedes calcular por separado el volumen de cada una de las figuras que la componen y después sumar esos resultados para hallar el volumen total.
Las fórmulas para calcular el volumen son:
- Volumen del prisma: área de la base por la altura
- Volumen del cilindro: área de la base por la altura
- Volumen de la pirámide: área de la base por la altura entre 3