Unidad 1. Actividad 3. ¿En abonos?
Escucha el audio que aparece a continuación.
Propósito:
multiplicarás y dividirás números con signo.
Reflexiona sobre las siguientes preguntas:
¿Has comprado a crédito o en abonos?
¿Los pagos que has realizado son fijos e iguales?
En ocasiones, la poca liquidez de nuestra economía nos obliga a comprar cosas en abonos. Generalmente, las tiendas que venden en abonos agregan un porcentaje de interés al precio final y lo dividen en un cierto número de pagos.
Analiza las siguientes situaciones y, utilizando números con signo, resuelve los ejercicios 14 a 16 de la Unidad 1, los cuales aparecen enseguida.
Unidad 1. Actividad 3. Ejercicio 14
Analiza la situación y realiza lo que se te pide.Si se establece como cero las 0 horas del día de hoy, ¿dónde ubicarías 3 semanas antes en una recta numérica?
¿Dónde 4 semanas después?
Ubica ![]() 3 y +4 en la siguiente recta numérica.
3 y +4 en la siguiente recta numérica.

y ahora una deuda de 100 pesos.
Escribe una operación que represente la siguiente situación: Juan planea ahorrar 100 pesos cada mes durante 6 meses. ¿Cuánto dinero ahorrará?
Escribe una operación que represente la siguiente situación: Los abonos del televisor son de 100 pesos. Juan todavía debe 6 pagos. ¿Cuánto dinero debe Juan?
Escribe una operación que represente la siguiente situación: Juan ha ahorrado 100 pesos cada mes durante los últimos 6 meses. ¿Cuánto dinero menos tenía hace 6 meses?
Ahora lee la siguiente regla de los signos en la multiplicación.
Ley de los signos
Para multiplicar dos números que tienen el mismo signo, se multiplican en ambos números y quedan con signo positivo.
Ejemplos:
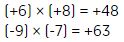
Para multiplicar dos números que tienen signo diferente, se multiplican ambos números y queda signo negativo.
Ejemplos:
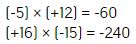
Analiza y compara las siguientes operaciones; después contesta las preguntas.

Con base en la información anterior, resuelve el Ejercicio 15.
Unidad 1. Actividad 3. Ejercicio 15
Responde las preguntas.a. Al dividir dos números que tienen el mismo signo, ¿qué signo le queda al cociente?
b. Al dividir dos números que tienen diferente signo, ¿qué signo le queda al cociente?
Escucha con atención el siguiente razonamiento acerca de la división de números con signo.
Si conozco el producto y uno de los factores de la multiplicación, entonces puedo encontrar el factor desconocido dividiendo el producto entre el factor conocido.
Esto es: a 15 multiplicado por 8 igual a 120, entonces 120 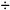 8
8 ![]() 15
15
Leo que:

Se observa que al dividir dos números que tienen el mismo signo, el resultado o cociente lleva signo positivo. Pero al dividir dos números que tienen signo diferente, el resultado o cociente lleva signo negativo.
Con base en la información anterior, resuelve el ejercicio 16 aplicando esta ley de los signos para la multiplicación y la división.
Unidad 1. Actividad 3. Ejercicio 16
Realiza mentalmente las siguientes operaciones. Después verifica tus resultados con la calculadora parlante.a. (+9) ![]() (+8)
(+8) ![]()
b. (+5) ![]() (-8)
(-8) ![]()
c. (-9) ![]() (11)
(11) ![]()
d. (+45) (-5) ![]()
e. (-60) (+3) ![]()
f. (-160) (-20) ![]()
En resumen, tenemos lo siguiente:
Multiplicación
El producto de dos factores con el mismo signo es positivo y el producto de dos factores con signo diferente es negativo, tenemos:
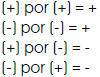
División
El cociente de dos números con el mismo signo es positivo y el cociente de dos números con diferente es negativo:
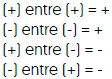
Escucha el tema “Números, números y más números” y después contesta las preguntas.
Por muy difícil que parezca, los números tienen una historia. Los primeros números, llamados naturales, surgieron por la necesidad de contar y de saber cuántos objetos había en un grupo.
Los números naturales, también llamados cardinales (1, 2, 3, 4…), son los más sencillos y son aplicables a las sumas de cantidades enteras, como personas y animales, en donde se obtienen nuevamente cantidades enteras. Otra operación en la que también es posible sumar cantidades enteras y obtener enteros, es la multiplicación.
Pero ten cuidado con la división, pues mientras que 10 dividido entre 2 es igual a 5, vemos que 2 dividido entre 10 es igual a . Así surge la fracción como una necesidad de dar solución a un problema y representarlo, es decir, escribirlo.
Representar la nada o la no existencia fue un importante paso para las matemáticas, el cero como número fue difícil de imaginar y de aceptar, pero finalmente forma parte de nuestra vida cotidiana.
Pero si piensas que, con los números naturales, las fracciones y el cero, se acaba la historia de los números, estás muy equivocado, pues por más difícil que sea imaginar el descubrimiento de nuevos números, así fue. “Los números negativos, las fracciones, los números irracionales, tuvieron que ser descubiertos, y la motivación para ello se debió, en cada caso, a la resolución de cuestiones que, de otro modo, hubieran quedado sin respuestas”, según Simón Singh.
En general, los matemáticos siempre han tenido que buscar nuevos números que les permitan resolver nuevas situaciones, pues al igual que algunas divisiones entre números naturales no se puedan resolver con un número natural, por lo que hay que recurrir a las fracciones, otras situaciones dieron origen a la existencia de los números negativos. Por ejemplo: al restar 7 de 5 la solución no es inmediata, por lo que para dar solución a este de problemas se necesitó incorporar la idea de los números negativos.
Un poco más difícil fue el “descubrimiento” de los números irracionales, los cuales obtienen su nombre del hecho de que no pueden estar representados por una fracción, y aunque en este módulo sólo trabajaremos con ellos en situaciones específicas, es necesario reconocer su importancia en la historia de los números.
Falta decir que, cuando los matemáticos creyeron haber encontrado todas las posibilidades que había con los números imaginarios, generaron una idea muy grande sobre lo que son los números y sus relaciones.
Presiona aquí para continuar