Unidad 1. Actividad 2. La atmósfera
Escucha el audio que aparece a continuación.
Propósito:
Sumarás y restarás números con signo.
¿Sabes a qué altura con respecto del mar vives? ¿Alguna vez has sentido los efectos del cambio de presión y de temperatura al viajar de un lugar a otro?
El planeta Tierra tiene una capa gaseosa llamada atmósfera. La atmósfera ejerce una presión sobre la Tierra y todo lo que en ella se encuentra; además, regula la temperatura en la superficie de la Tierra.
La temperatura y la presión del aire cambian con la altura (altitud). Aunque la temperatura no depende sólo de la altura, sino del tipo de suelo y de las nubes, entre otros factores.
Es importante mencionar que la presión se mide en milímetros de mercurio y su abreviatura es: mmHg.
Resuelve los ejercicios 7 y 8 de la Unidad 1, que aparecen enseguida.
Unidad 1. Actividad 2. Ejercicio 7
Escucha la siguiente información y después contesta:Altura en metros con respecto al nivel del mar: 4000
Presión en milímetros de mercurio: 462.3
Temperatura en grados centígrados: ![]() 11.0
11.0
Altura en metros con respecto al nivel del mar: 2000
Presión en milímetros de mercurio: 596.2
Temperatura en grados centígrados: 2.0
Altura en metros con respecto al nivel del mar: 0.0
Presión en milímetros de mercurio: 760
Temperatura en grados centígrados: 15.0
Tomando como base la información anterior, contesta las siguientes preguntas:
¿A qué altura con respecto al nivel del mar hay mayor presión atmosférica?
¿Qué altura con respecto al nivel del mar es posible encontrar una temperatura de
¿Cuál es la diferencia entre la temperatura medida a 2000 metros de altura y la medida a 4000?:
Unidad 1. Actividad 2. Ejercicio 8
Escucha la información y responde las preguntas:Las integrantes de una cooperativa que hacen muñecas compararon los precios a los que compraban el año pasado sus materiales con el precio al que los consiguen este año.
Tenemos los siguientes datos:
Material: listón
Cantidad: un rollo
Año anterior: 75 pesos
Año actual: 89 pesos
Variación: +14 pesos
Material: botones
Cantidad: docena
Año anterior: 6 pesos
Año actual: 5 pesos
Variación: ![]()
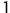 peso
peso
Material: dubetina
Cantidad: un metro
Año anterior: 25 pesos
Año actual: 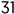 pesos
pesos
Variación: +6 pesos
Material: hilo
Cantidad: un carrete
Año anterior: 7 pesos
Año actual: 5 pesos
Variación: ![]() 2 pesos
2 pesos
Con base en la información anterior, responde las siguientes preguntas:
Comparado con el año pasado, ¿cuánto más cuesta el rollo de listón este año?
¿Cuánto bajó de precio el carrete de hilo?, ¿por qué el cambio está representado con un signo negativo?
¿La cooperativa tendrá que subir o bajar el precio de las muñecas?
¿Por qué?
Escucha el audio que aparece a continuación. En ella conocerás la ley de los signos.
Escucha con atención la explicación sobre la ley de los signos.
El valor absoluto de un número, es la distancia de dicho número con respecto al origen, es decir, al cero. Por ejemplo, el valor absoluto de 5 y -5 es 5, porque ambos se encuentran a 5 unidades del origen.
-5 -4 -3 -2 -1 0 1 2 3 4 5
Para sumar dos números con el mismo signo, se suman ambos números y se deja el mismo signo.
Ejemplos:
(+9) + (+7) = +16
(-9) + (-7) = -16
Para sumar dos números con signo diferente, se resta el número de menor valor absoluto al de mayor valor absoluto y se deja el signo del número de mayor valor absoluto.
Ejemplo:
(-5) + (+12) = +7
Toma en cuenta que:
En los próximos ejercicios te encontrarás con el uso del paréntesis, recuerda que los puntos para abrir paréntesis son 1, 2, 6 y para cerrar paréntesis son 3, 4, 5.
Ahora, con esta información, resuelve los ejercicios 9 a 13 de la Unidad 1, que aparecen enseguida.
Unidad 1. Actividad 2. Ejercicio 9
Realiza las siguientes sumas, aplicando la ley de los signos.
Unidad 1. Actividad 2. Ejercicio 10
Analiza el talón de pago de Rosalía y realiza lo que se pide a continuación:Talón de pago del trabajador.
Páguese a: Rosalía Sánchez González
Mes: 09 Día: 30 Año: 16
Número de filiación: 0126445245-003
GPO 1/1
Periodo de pago: 15 de septiembre de 2015 a 30 de septiembre de 2016
Concepto: sueldo
Importe: 2130.35 pesos
Concepto: impuesto sobre la renta
Importe: ![]() 213.03 pesos
213.03 pesos
Concepto: ayuda vivienda
Importe: 45 pesos
Concepto: seguro social
Importe: ![]() 120.12 pesos
120.12 pesos
Concepto: Caja de ahorro
Importe: ![]() 105 pesos
105 pesos
Considerando los datos anteriores, responde estas preguntas.
¿Qué conceptos representan ingresos para Rosalía?
¿Cuánto le pagan por dichos conceptos?
¿Con cuántos conceptos le hacen descuentos?
¿Cuánto le descuentan en total?
¿Cuánto dinero cobró Rosalía en la quincena?
Unidad 1. Actividad 2. Ejercicio 11
Escucha y responde:Las fechas de nacimiento de algunos matemáticos importantes son:
Gauss, año 1777 de nuestra era.
Pitágoras, año 572 antes de nuestra era.
Eratóstenes, año 273 antes de nuestra era..
Pappus, año 300 de nuestra era.
Euclides, año 300 antes de nuestra era.
En la forma de recta numérica ubica las fechas de nacimiento de los matemáticos en el tiempo. Recuerda que el nacimiento de Jesucristo fue en el año 0, pues marca el inicio de la nueva era, de tal modo que a. e. significa antes de nuestra era y n. e. significa nuestra era.
Escribe las fechas de nacimiento de los matemáticos usando los signos
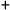 y
y Calcula cuántos años han pasado del nacimiento de cada uno de los matemáticos a la fecha.
Gauss:
Pitágoras:
Eratóstenes:
Pappus:
Unidad 1. Actividad 2. Ejercicio 12
Estudia y compara las siguientes sumas y restas:
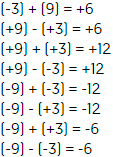
Después de haber revisado los ejemplos anteriores, contesta las siguientes preguntas.
¿Qué resultado obtienes al sumar -3 a 9?
¿Y cuál si restas +3 al mismo número?
¿Qué resultado obtienes al sumar +3 a 9?
¿Y cuál si restas -3 al mismo número?
Escucha con mucho cuidado la siguiente aclaración.
Para restar números con signo, se cambia el signo del sustraendo y se procede como en la suma de números con signo.
Ejemplos:
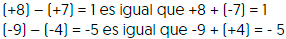
Aplicando esta aclaración, resuelve el ejercicio 13.
Unidad 1. Actividad 2. Ejercicio 13
Realiza las siguientes restas.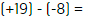
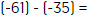
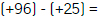
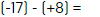
Escucha el siguiente resumen:
Para sumar dos números de igual signo, se suman los números y queda el mismo signo.
Ejemplo:
(![]() 39) + (
39) + (![]() 10)
10) ![]()
![]() 49
49
Para sumar dos números con diferente signo, se resta el número de menor valor absoluto al de mayor valor absoluto y queda el signo del número de mayor valor absoluto.
Ejemplo:
(![]() 45) + (+25)
45) + (+25) ![]()
![]() 20
20
Para restar números con signo, se cambia el signo del sustraendo, en forma mental o escrita, y se procede como con la suma.
Ejemplo:
Para restar
Minuendo: ![]() 19
19
Signo: ![]()
Sustraendo: ![]() 7
7
Resta o diferencia: ![]() 12
12
Si se cambia en forma escrita, tenemos:
(![]() 19) + (+7)
19) + (+7) ![]()
![]() 12
12