Unidad 6. Actividad 18. Yoloxóchitl
Escucha el audio que aparece a continuación.
Propósito:
Resolverás problemas que involucran un sistema de ecuaciones con dos incógnitas mediante métodos de sustitución y de suma o resta.
¿Perteneces a alguna cooperativa? ¿Qué sabes acerca de las cooperativas y de las ventajas que ofrecen a sus integrantes? Coméntalo con tu asesor o asesora.
Las dificultades que los pequeños productores o consumidores tienen para comercializar sus productos o para comprar materia prima les obliga a asociarse en cooperativas.
Las ventajas que las cooperativas ofrecen a sus asociados van desde la posibilidad de comprar a menor precio la materia prima hasta vender sus productos a mejores precios.
Resuelve el ejercicio 1 de la Unidad 6, que aparece enseguida.
Unidad 6. Actividad 18. Ejercicio 1
Escucha la situación y analiza el procedimiento.
Gabriela es tesorera de la cooperativa Yoloxóchitl, en la cual solo elabora tapetes de dos tamaños. El precio de los tapetes chicos es de 220 pesos, y el de los grandes, 400 pesos.
Al hacer su relación de ventas del día de ayer, le dijeron a Gabriela que en total habían vendido 14 piezas de tapetes de los dos tamaños y reunido 4520 pesos.
¿Cuántos tapetes de cada tamaño vendieron?
Tenemos el siguiente planteamiento:
Se vendieron 14 tapetes obteniendo un total de 4520 pesos.
El tapete chico costó 220 pesos.
El tapete grande costó 400 pesos.
Para el tapete chico le asignaremos ![]() .
.
Para el tapete grande asignaremos .
Para el planteamiento, tenemos dos ecuaciones: una expresa la cantidad de objetos y otra que relaciona los objetos con el precio:
Despejamos :
Realizamos las operaciones y obtenemos:
Finalmente, comprobamos:
6 + 8 ![]() 14
14
220 por (6) + 400 por (8) ![]() 4520
4520
4520 ![]() 4520
4520
Escucha el audio que aparece a continuación.
En la operación de 220(14 - y), la explicación de este paso es: la multiplicación de un número por la suma de dos o varios sumandos es igual que multiplicar ese número por cada uno de los sumandos y después hacer la suma de los productos. A esta propiedad numérica se le llama propiedad distributiva de la multiplicación con respecto a la suma y a la resta.
En la resolución de ecuaciones por el método de sustitución con un sistemas de dos ecuaciones con dos incógnitas de primer grado, se inicia despejando una variable y encontrando su valor en términos de la otra. En el ejemplo anterior se dijo que x = 14 – y; luego se sustituye dicho valor en la segunda ecuación y se obtiene una ecuación con una incógnita, la cual se resuelve de la forma ya conocida.
Una vez encontrado el valor de la incógnita en la segunda ecuación se sustituye en la primera, quedando una ecuación con una incógnita, la cual se resuelve de la forma ya mencionada.
Al final se comprueba sustituyendo el valor encontrado para cada incógnita en las dos ecuaciones iniciales.
Resuelve los ejercicios 2 a 5 de la Unidad 6, que aparecen enseguida.
Unidad 6. Actividad 18. Ejercicio 2
La entrada al circo cuesta 65 pesos para adulto y 35 pesos para niño. Hoy se recaudaron diezyocho mil novecientos noventa y cinco pesos por 439 boletos vendidos.
Plantea las dos ecuaciones: una en términos de boletos vendidos y otra en términos del dinero recaudado.
¿Cuántos boletos para adulto vendieron y cuántos para niño?
Unidad 6. Actividad 18. Ejercicio 3
Entre dos hermanos recibieron 6500 pesos. Si el menor recibió 800 pesos menos que el mayor, ¿cuánto recibió cada uno?
Unidad 6. Actividad 18. Ejercicio 4
Escucha y analiza el procedimiento.
Una caja de quesos pesa 51.6 kilogramos. Si en total trae 27 quesos de 1.6 kilogramos y 2.3 kilogramos, ¿cuántos quesos de cada peso trae?
Escucha la siguiente explicación de cómo resolver ecuaciones simultáneas por suma o resta.
Hay que sumar o restar los términos semejantes de ambas ecuaciones, de tal forma que se elimine una incógnita:
Se resuelve la ecuación obtenida: 13 ![]()
![]() 104
104
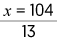
![]()
![]() 8
8
Una vez conocido el valor de una incógnita, se sustituye en cualquiera de las dos ecuaciones iniciales y se resuelve la ecuación obtenida.
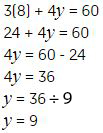
Para comprobar se sustituyen los valores obtenidos en las ecuaciones iniciales:
En caso de que ninguna incógnita tenga igual el valor absoluto de sus 2 coeficientes, puede multiplicarse alguna de las ecuaciones por el número que sea necesario para que los dos coeficientes de alguna de las incógnitas tengan el mismo valor absoluto.
Ejemplo:
Se puede multiplicar la ecuación b por 2 y obtener lo siguiente:
Con lo que queda el siguiente sistema de ecuaciones:
Unidad 6. Actividad 18. Ejercicio 5
Resuelve las ecuaciones, encuentra el valor de