Lee el siguiente texto.

En la actividad anterior dejaste planeadas tus sesiones de las palabras generadoras que desarrollarás en la fase 2, ahora prepararás las sesiones de matemáticas, pero antes, y con la intención de entrar en materia, te invitamos a resolver los dos problemas siguientes.

1. Doña Juanita tiene que comprar naranjas o mandarinas para hacer jugo. Ayúdale a decidir si le conviene más hacer jugo de naranja o de mandarina. Analiza los precios y la cantidad de mandarinas o naranjas que se venden por ese precio.

En estos problemas se utilizan otros signos para representar los números que conoces.

Lee el siguiente texto.

Es evidente que tú sabes resolver problemas aritméticos tan sencillos como los anteriores, incluso más complejos, y que la dificultad con la que te enfrentaste fue el desconocimiento de la escritura convencional de esos signos numéricos, por lo que no pudiste, al principio, interpretar ni comparar las cantidades, aún cuando los números implicados eran pequeños, es decir, estaban en un rango del 1 al 100.

También pudiste constatar que haciendo una relación entre la serie numérica oral que ya conoces y la escritura de esos números, en el orden que se presentan en las tiras numéricas, pudiste identificar y escribir esos números. Además, si se te olvidaba algún número recurriste a tu tira numérica, para volver a ubicar el número que necesitabas, sin necesidad de preguntar a otra persona.

Esto mismo sucede con las personas que se alfabetizarán, saben contar usando la serie numérica oral pero, probablemente, desconocen la escritura de la serie numérica escrita, por lo que será mucho más sencillo que las personas jóvenes o adultas, aprendan la escritura de los números del uno al 100 si se la presentas en bloque, es decir, en rangos numéricos, del 1 al 10, o del 1 al 15, usando tiras numéricas, y del 1 al 100, utilizando la cuadrícula numérica, porque podrán analizar las relaciones que se dan entre ellos.

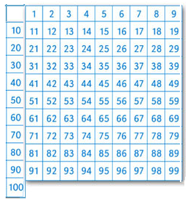El hecho de que observen cómo se combinan los primeros 10 dígitos (0, 1, 2, 3, 4, 5, 6, 7, 8 y 9) para formar todos los demás números, distribuidos en las filas y columnas de la cuadrícula numérica, les facilitará el aprendizaje de los mismos, además, ellos mismos podrán recurrir a estos recursos cuando no sepan escribir algún número. Este análisis no se logra si les propones que vayan aprendiendo, por sesión, cada uno de los números, es decir, hoy aprenden el uno, mañana el dos, luego el tres, y así hasta un número determinado.

Lee el siguiente texto.

La intención principal de esta actividad fue demostrarte la importancia que tiene el uso de las tiras y las cuadrículas numéricas en el aprendizaje de la escritura de los números. Úsalas cuando trabajes los contenidos de matemáticas.

Es probable que entre las personas que atiendas haya quienes ya sepan escribir los números del 1 al 100. Será importante que reconozcas y valores estos conocimientos públicamente, para que les des confianza y mejoren su autoestima, al saberse reconocidos. Propón a estas personas situaciones que tengan números más grandes, como precios de ropa o zapatos o los recibos de luz, agua, etc. Muéstrales una cuadrícula numérica en un rango mayor para que los reconozcan y los usen.

En la sección Para saber más, encontrarás una cuadrícula numérica hasta el cien y actividades que podrás realizar con estos educandos.

También será importante que les pidas que apoyen a sus compañeros que todavía no reconocen los números del 1 al 100, esta situación también les proporcionará gusto al saberse útiles a otras personas.