Unidad 8. Actividad 23. Evalúa tu masa corporal
Escucha el audio que aparece a continuación.
Has oído hablar del Índice de Masa Corporal (IMC)? ¿Sabías que el IMC te indica si tienes problemas de sobrepeso o de obesidad? ¿Sabes cómo calcularlo? Coméntalo con tu asesor o asesora.
La obesidad es un problema de salud pública que va en aumento. Por ello es importante cuidar la cantidad y calidad de los alimentos que consumimos. El Índice de Masa Corporal se calcula a partir de la talla en metros y del peso de la persona en kilogramos.
Verónica leyó la siguiente información en el periódico:
Comer bien ayuda a perder peso
Por Silvia Ojanguren
Cómo evaluar la masa corporal
Por principio de cuentas, la gente tiene que evaluar si es parte de la estadística de sobrepeso y obesidad, para lo cual debe conocer su IMC, es decir, el índice de masa corporal, que se obtiene así:
el peso en kilogramos se divide entre el cuadrado de la estatura en metros.
Vamos a calcular nuestro IMC, el cual nos dice si nuestro peso pone en riesgo nuestra salud y en peligro nuestra vanidad.
Normal: IMC de 18.6 a 24.9
Sobrepeso: IMC de 25.0 a 26.9
Obesidad I: IMC de 27.0 a 29.0
Obesidad II: IMC de 30.0 a 34.9
Obesidad III: IMC de 35.0 a 40.0
Los índicesa anteriores son para mujeres que miden 1.50 m o más y hombres que miden 1.60 m o más.
Resuelve los ejercicios 1 a 8 de la unidad 8, que aparecen enseguida.
Unidad 8. Actividad 23. Ejercicio 1
Utiliza la letra
para representar el IMC, es decir, el índice de masa corporal, la 
para representar el peso y la 
para representar la estatura. Escribe la ecuación para calcular el IMC.
a. Verónica pesa 67 kilogramos y mide 1.52 metros, ¿cuál es su IMC?
b. ¿Verónica tiene problemas de sobrepeso o de obesidad?
Escucha la siguiente explicación.
Unidad 8. Actividad 23. Ejercicio 2
Ramón tiene un IMC de 24.38 y pesa 68 kilogramos. ¿Cuál es su estatura?
Escribe la ecuación donde despejó que es el peso y despeja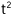 
, que es la estatura al cuadrado.
Sustituye las medidas de Ramón y calcula :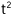
Del valor obtenido en el inciso anterior, calcula la estatura de Ramón. Si tu calculadora trae raíz cuadrada, puedes obtenerla directamente.
Escucha con atención la siguiente explicación.
Analiza cómo se calcula la raíz cuadrada del número 678.
Se separan las cifras de dos en dos, empezando por la derecha.
Raíz cuadrada de 678
Se busca un número que, multiplicado por sí mismo, sea igual o casi igual, pero menor que el número formado por la cifra de la izquierda, 6, y se escribe sobre la línea derecha.
El número encontrado: 2 se multiplica por sí mismo y el resultado se resta del 6.
Aquí tenemos que a 678, al 6 le restamos 4 y nos quedan 2.
Dentro de la raíz, se baja el segundo par de cifras. En el exterior, se duplica el número de la primera línea y el resultado se escribe en una segunda línea, abajo.
Al lado del número 2, escribimos 78, que son los números que faltan:
Se busca una cifra, 6, que se agrega a los números de la primera y segunda líneas de la raíz. La multiplicación de dicha cifra por el número de la línea de abajo 46 debe ser igual o casi igual, pero menor que 278. Se escribe el resultado de la multiplicación y se resta a 278.
Entonces a 278 se le resta 276, que sale de 6 
6 = 36, el número 6 lo escribimos debajo del 8, y el número 3 lo sumamos a la multiplicación de
6 4 = 24 más 3 nos da 27.
Al realizar la resta de 278 y 276, nos quedan 3.
El resultado final es 26 y quedan 2. Se comprueba multiplicando 26 por sí mismo y sumando 2:
Unidad 8. Actividad 23. Ejercicio 3
El área de un quiosco circular es de 200.96 metros cuadrados; ¿Cuánto mide su radio?
Recuerda que la fórmula para calcular el área del círculo es 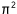A
a 
(pi) se le considera con el valor de 3.14.
Despeja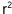 
de la fórmula.
Sustituye los valores y encuentre los valores de
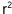
:Ahora lee con atención la siguiente explicación.
Las ecuaciones pueden tener alguna literal elevada a una potencia.
Ejemplo:
Para conocer el valor 
, primero hay que despejarla de la ecuación y realizar las operaciones indicadas:
Finalmente, hay que sacar la raíz cuadrada a ambos miembros de la ecuación, es decir, raíz cuadrada de 
y raíz cuadrada de 25.
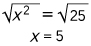
Unidad 8. Actividad 23. Ejercicio 4
Calcula el valor de la incógnita de las siguientes ecuaciones.
Escucha la explicación del teorema de Pitágoras y explora los triángulos.
Teorema de Pitágoras
Un triángulo rectángulo es aquel que tiene un ángulo recto de 90 grados. El lado opuesto al ángulo recto es llamado hipotenusa; los dos lados que forman el ángulo recto son llamados catetos.
Pide a tu asesor que te muestre el triángulo rectángulo que corresponde a este ejercicio, el cual se encuentra en los materiales en relieve.
Realiza la figura y las indicaciones de la figura en relieve de puntos
En un triángulo rectángulo, el área del cuadrado construido sobre el lado opuesto al ángulo recto es igual a la suma de las áreas de los cuadrados construidos sobre los lados que forman el ángulo recto.
Algebraicamente, puede expresarse como: 
al cuadrado es igual a 
al cuadrado más b al cuadrado, o 
Si en un triángulo rectángulo llamamos a la hipotenusa y y 
a cada uno de los catetos, entonces:
Como al cuadrado es igual a al cuadrado más al cuadrado, al obtener la raíz de de esta ecuación tenemos que es igual a la raíz de al cuadrado más al cuadrado.
Si queremos despejar a de la ecuación original, tenemos que al cuadrado es igual a la raíz de al cuadrado menos al cuadrado.
Si queremos despejar a de la ecuación original, tenemos que al cuadrado es igual a la raíz de al cuadrado menos al cuadrado.
Pide a tu asesor que te dé a palpar un triángulo rectángulo que está unido a un cuadrado por cada uno de sus lados. Se encuentra en los materiales en relieve que corresponden a este ejercicio.
Realiza la figura y las letras en relieve de puntos.
Unidad 8. Actividad 23. Ejercicio 5
Lety necesita construir el techo de la casa de asistencia; para calcular la medida de las vigas, necesita aplicar el teorema de Pitágoras, ya que el techo va a ser de lámina en forma de dos caídas, conocida como dos aguas.Lety dice que el ancho de la casa es de 8 metros y la parte central va a medir 2 metros por encima de los lados. El teorema de Pitágoras solo se aplica a triángulos rectángulos; pero si dividimos en dos el triángulo formado por el techo, quedarán dos triángulos rectángulos. Podemos calcular por partes.
El teorema de Pitágoras es al cuadrado es igual a al cuadrado más al cuadrado, es decir:
Pide a tu asesor que te dé la figura del techo de la casa: se trata de dos triángulos rectángulos unidos por el ángulo de noventa grados. Se encuentra en los materiales en relieve que corresponden a este ejercicio.
Realiza la figura y las indicaciones en relieve de puntos.
Pero solo tomaremos la mitad de esta figura, es decir, un triángulo rectángulo, donde un lado mide 2 metros y otro mide 4 metros.
Al sustituir los datos en el teorema tenemos:
al cuadrado es igual a a al cuadrado más b al cuadrado
al cuadrado es igual a 2 al cuadrado más 4 al cuadrado
al cuadrado es igual a 4 más 16
al cuadrado es igual a 20
Para conocer el valor de hay que sacar la raíz cuadrada a ambos miembros de la ecuación:
Raíz cuadrada de cuadrada es igual a la raíz cuadrada de 20.
Raíz de al cuadrado es igual a la raíz de 20: 
Cada viga debe medir 4.47 metros las dos juntas 8.94 metros.
Unidad 8. Actividad 23. Ejercicio 6
Escucha el problema y contesta.
Lety y Paty, junto con otras compañeras, planean hacer un área de juego para sus hijos. La estructura para la escalera de una resbaladilla lleva dos piezas de la siguiente forma.
Pide a tu asesor que te dé a palpar una figura en forma de triángulo rectángulo con un ángulo de 90 grados. Se encuentra en los materiales en relieve que corresponden a este ejercicio.
Realiza la figura y el número en relieve de puntos.
La altura debe ser de 2.5 metros y la base debe medir 1.3 metros. ¿Qué cantidad de tubo se requiere para cada una de las estructuras?
¿Puedes aplicar el teorema de Pitágoras para calcular la medida que desconoces?
¿Cuál es la medida del lado desconocido?
¿Qué cantidad de tubo se requiere para cada una de las estructuras?
Unidad 8. Actividad 23. Ejercicio 7
El recíproco del teorema de Pitágoras dice que en un triángulo, cuando el área del cuadrado construido sobre el lado mayor es igual a la suma de las áreas de los cuadrados construidos sobre los otros lados del mismo triángulo, entonces el triángulo es rectángulo.Prueba que los siguientes triángulos son rectángulos. Si es un triángulo rectángulo, debe cumplir el teorema de Pitágoras.
Triángulo 1, la hipotenusa mide 5 centímetros y los catetos miden 3 y 4 centímetros, respectivamente.
Triángulo 2, la hipotenusa mide 12.8 centímetros y los catetos miden 8 y 10 centímetros respectivamente.
Unidad 8. Actividad 23. Ejercicio 8
Escucha el problema y contesta las preguntas.
En un muro de contención de forma rectangular metieron estructuras metálicas como refuerzo. Estas estructuras atraviesan el muro de tal manera que forman una cruz en medio. El largo de cada estructura es de 10 metros y la altura del muro es de 6 metros. ¿Cuánto mide el ancho del muro?
Pide a tu asesor que te muestre la figura rectangular del muro; los refuerzos están en el interior de la figura y se cruzan en medio formando una cruz. Se encuentra en los materiales en relieve que corresponden a este ejercicio.
Con base en la información, imagina y describe el triángulo que relaciona los datos.
¿Cómo es el ángulo opuesto al lado más largo de dicho triángulo?
Si tienes que hacer algún despeje, hazlo.