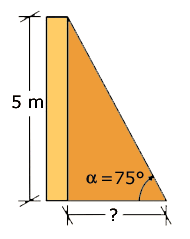
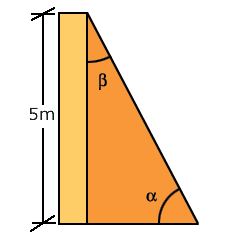
Juan es maestro albañil; tiene que construir una barda de 25 m de largo y 5 m de altura. Para que no se caiga, debe colocar a cada 5 m un refuerzo con un ángulo en su base de 75° con el piso, como se muestra en el croquis:
 |
El ángulo de
inclinación (
¿Cómo puede Juan saber cuánto debe estar separado el sostén del muro? |
Juan resuelve su problema de la siguiente manera:
1. En un transportador, señala el valor de 75°.
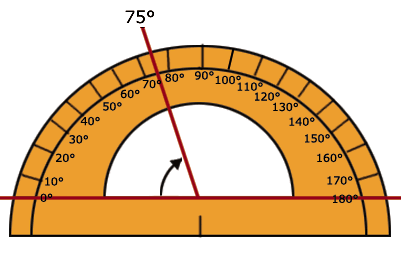
2. Una vez que tiene marcado en el transportador el valor de 75°, en la parte superior del muro fija un extremo de un carrete de cáñamo y lo deja caer hasta la base del muro.
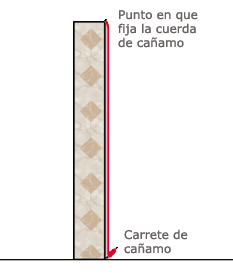
3. Separa el carrete de cáñamo de la base del muro liberando cuerda conforme se aleja del muro y con el transportador va midiendo el ángulo que se forma entre el piso y la cuerda de cáñamo.
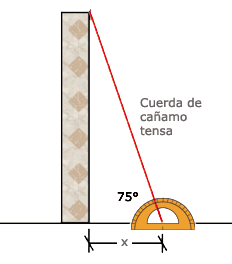
4. Cuando la cuerda de cáñamo y el piso forman el ángulo de 75°, pone una marca en el piso y mide cuánto hay de esa marca a la base del muro.
Después de hacer todo esto, Juan puede decir que de la base del muro a la orilla del refuerzo debe haber aproximadamente 1.34 m.
Con todo esto, Juan resulta muy cansado, pues tuvo que hacer muchas maniobras para calcular este cateto del triángulo rectángulo que forma el refuerzo, por lo que decide mejor utilizar la trigonometría, que significa la medida de los ángulos.
Para usar mejor la trigonometría, es necesario poner nombre a cada una de las partes de un triángulo rectángulo.
Así se tiene que:
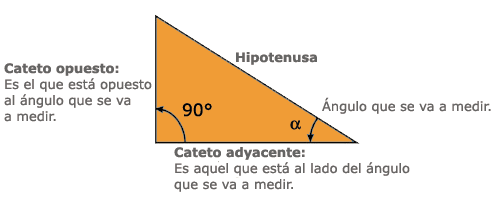
También podría ser así:
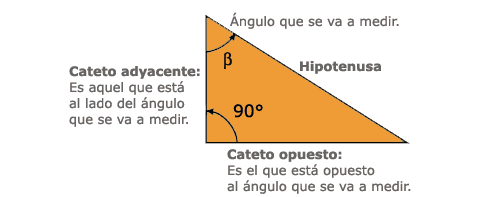
Ahora es necesario determinar una función que relacione el ángulo, los catetos y la hipotenusa del triángulo, para ello haga lo siguiente:
1. Coloque el transportador en un eje "x" con un hilo de longitud de un decímetro (10 cm).
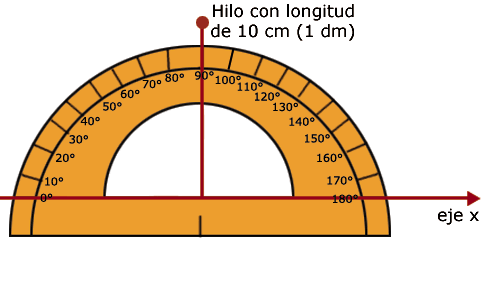
2. Se mide la proyección del extremo del hilo sobre el eje "x" al variar el ángulo del hilo. (La variación fue 90°, 67.5°, 45°, 22.5°, 0°.)
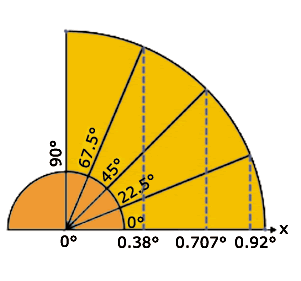
3. Se obtuvo lo siguiente:
| Ángulo |
x(dm) |
90° |
0 |
67.5° |
0.38 |
45° |
0.707 |
22.5° |
0.92 |
| 0° |
1 |
En este experimento sólo se probó con 5
ángulos: 90°, 67.5°,
45°, 22.5° y
0°, se obtuvieron 5
valores de "x" pero se podría haber
probado con "n" ángulos y se habrían
obtenido "n" valores de "x".
Lo importante es que para cada ángulo siempre corresponderá
un valor de "x".
Hagamos el análisis de un solo triángulo de los obtenidos, el de 45°.
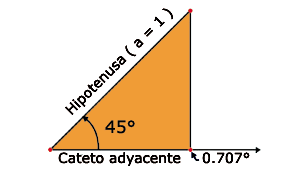
Para identificar la función que relacione el ángulo
,
el cateto adyacente y la hipotenusa, se ha definido la función
llamada coseno, que se abrevia "cos".
Esta función (cos) relaciona al cateto
adyacente entre la hipotenusa, por lo que se puede escribir que:
| |
Así, siempre que se diga coseno (cos) de 45°, se tendrá 0.707 y esto es producto de dividir al cateto adyacente entre la hipotenusa de un triángulo rectángulo.
Para osbtener los valores del coseno (cos)
de diferentes ángulos (cos),
existen tablas que dan los valores aproximados, o también se pueden
utilizar calculadoras que tienen funciones trigonométricas.
El coseno de los ángulos, de 5 en 5 grados, se presenta a continuación en la siguiente tabla.
ángulo  |
cos |
0 |
1 |
5 |
0.996 |
10 |
0.985 |
15 |
0.966 |
20 |
0.940 |
25 |
0.906 |
30 |
0.866 |
35 |
0.819 |
40 |
0.766 |
45 |
0.707 |
50 |
0.643 |
55 |
0.574 |
60 |
0.5 |
65 |
0.423 |
70 |
0.342 |
75 |
0.259 |
80 |
0.174 |
85 |
0.087 |
90 |
0 |
Con una calculadora, para obtener la función trigonométrica de un ángulo, se hace lo siguiente:
Cálculo del coseno de 36°.
El coseno de 36° es 0.8090169.
| Cos 36° = 0.809
|
Por lo regular sólo se usan tres decimales.
 |
Las funciones trigonométricas más utilizadas son el seno (sen), el coseno (cos) y la tangente (tan). |
El seno es la relación que existe entre el cateto opuesto y la hipotenusa.
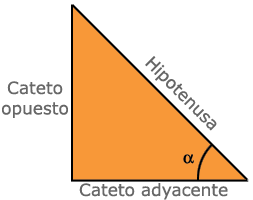
La tangente es la relación que existe entre el cateto opuesto y el cateto adyacente.
|
Así como para el coseno, existen tambien que se han construuido para el seno y la tangente de un ángulo. A continuación se presenta una tabla con lo senos, cosenos y tangentes de ángulos de 0° a 90°, de 1 grado en 1 grado |
| Sen 30° = 0.5 | (Ver en la tabla el renglón 30°
y luego buscar la columna sen
y ahí se encuentra el 0.5.) |
Presione el siguiente botón y realice la actividad que se propone.
En el caso de las tangentes (tan) sucede algo parecido.
Tangente de 15° = 0.268 |
Para esto, se busca 15° en
la primera columna, la de los grados ,
siguiendo el renglón hasta la columna tan.
El cruce es el valor de la tangente de 15°.
Observe usted, en el siguiente dibujo, como Juan, sin tener que subir al muro, ni tender la cuerda de cáñamo, ahora puede calcular todas las dimensiones y ángulos del soporte de su muro.
Juan sabe que el muro debe tener un ángulo
de 75° y que el cateto opuesto a ese ángulo
(la altura del muro) es de 5 m. Con eso es
suficiente para calcular:
 |
a) El cateto adyacente al ángulo
a (que es lo que anda buscando). |
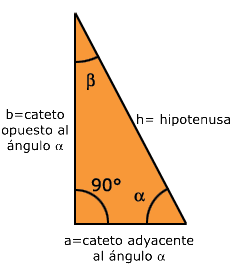
| Para lo anterior, Juan identifica perfectamente cada una de las partes de su triángulo rectángulo. | Su triángulo con los datos que conoce se ve así: |
 |
 |
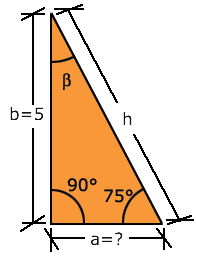Como puede usted observar, se conoce el ángulo
que es igual a 75°, se conoce el cateto opuesto
que es de 5 m y se busca el cateto adyacente,
por lo que se deberá identificar a una función trigonométrica
que contenga a ,
al cateto opuesto y al cateto adyacente.
Recordando a las tres funciones trigonométricas que se han visto, se tiene:
 |
La función que incluye a ,
al cateto opuesto (b) y al cateto adyacente
(a) es la tangente (tan).
 |
Como =
75° y el cateto opuesto (b) es 5,
se tiene:
 |
Para despejar "a", se multiplican ambos miembros por "a":
 |
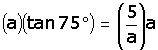Y luego se divide, también a ambos términos, entre tan75°:
 |
Con lo que se obtiene:
 |
Con una tabla o con una calculadora, se obtiene que tan 75° = 3.732, por lo que este valor se puede sustituir en la ecuación obtenida.
 |
Con lo que Juan obtiene que el soporte estará separado de la base del muro aproximadamente 1.34 m.
Observe usted que es lo mismo que obtuvo con la cuerda de cáñamo.
Ahora decide que va a obtener la longitud de la hipotenusa (la longitud de la parte superior del soporte). Lo que puede lograr por dos caminos:
1. Por medio de las funciones trigonométricas.
2. Por medio del teorema de Pitágoras.
Por medio de las funciones trigonométricas, lo
que tiene que hacer es encontrar una función que relacione al ángulo
()
con cualquiera de los catetos (porque ahora conoce los dos) y la hipotenusa.
De acuerdo con las funciones trigonométricas que conocemos, se tiene:
|
Cualquiera de las dos primeras funciones (sen y cos) pueden ayudar a Juan a conocer la hipotenusa. Tomemos al seno.
 |
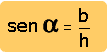| Se despeja a la "h"
(hipotenusa) que es lo que se busca. Primero, se multiplican ambos
términos por "h" y, luego, se
dividen también a ambos términos entre "sen
": |
Se sustituyen los valores
conocidos de=
75° y b = 5. |
 |
 |
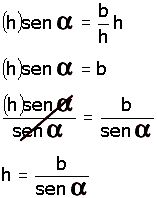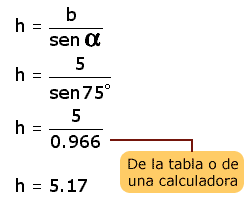Esto quiere decir que la parte superior del soporte del muro de Juan medirá 5.17 m.
Por el teorema de Pitágoras, se tiene que:
 |
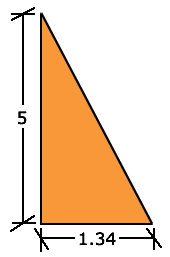Se conocen los catetos "a" y "b" y se desconoce la hipotenusa h. El teorema de Pitágoras señala que:
Se sustituye el valor de a = 1.34 y el de b = 5, se tiene que:
|
Se saca la raíz cuadrada en ambos miembros de la ecuación, se tiene que:
 |
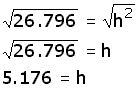Esta cantidad es muy parecida a la que se obtuvo por medio de las funciones trigonométricas (5.17).
Ahora Juan ha decidido que va a calcular el ángulo
superior (
)
del soporte con el muro. También se puede obtener por varios caminos
pero utilicemos uno directo que es el de las funciones trigonométricas.
Se dice que es un camino directo porque ya se conocen las dimensiones de los dos catetos y la hipotenusa. Así que con plantear cualquier función se obtendrá el valor del ángulo que se busca.
 |
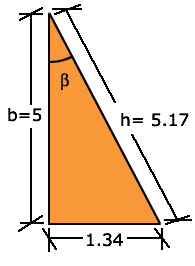Observe que cambiaron de como
se usaban con Así que las funciones trigonométricas serán:
|
Utilizando cualquiera de las tres funciones, se puede
obtener el valor de ;
en este caso se usa sen .
 |
Se obtiene de la tabla el ángulo cuyo sen es 0.259,
o sea, se busca en la columna de sen la cantidad 0.259
y se obtiene en la columna que dice 15°,
esto quiere decir que el ángulo cuyo seno es 0.259
es 15°.
El ángulo superior del muro y su soporte es de 15°.
Otra manera, la más simple de todas, es que sabemos que la suma de los tres ángulos de un triángulo siempre es igual a 180°.
Así que 180 = 90 + 75 + ;
por lo tanto,
= 15°.
Las funciones trigonométricas tienen muchas aplicaciones.
| Se tiene a la vista el
campanario de la iglesia de Gutiérrez Zamora, Veracruz, y se
está en una planicie en la que se pueden recorrer 50
m sin ningún problema.
¿Cómo obtendría la distancia que hay desde donde se encuentra hasta la iglesia de Gutiérrez Zamora? Se recomienda que siempre dibuje un triángulo rectángulo. El observador se movió 50 m a la derecha del primer punto de observación porque ésta es la distancia que se lo permite el terreno. |
 |
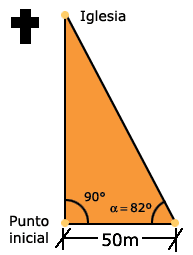Ahora se cuenta con un triángulo rectángulo
con un ángulo
de 82° y un cateto adyacente a ese ángulo
que mide 50 m.
Se requiere una función que incluya al ángulo
,
al cateto adyacente y a la hipotenusa.
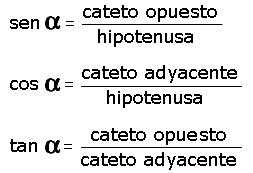
| Recordando las funciones del sen, cos y tan, se tiene: |
 |
| La función que incluye lo que busca (la hipotenusa)
y lo que tiene (el ángulo
y el cateto adyacente) es el coseno. |
 |
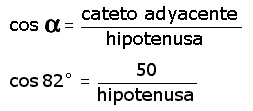Para despejar la hipotenusa, se multiplica por la hipotenusa a los dos miembros y luego se divide, también a los dos miembros, entre el coseno de 82°.
 |
De las tablas de funciones trigonométricas o con una calculadora con funciones trigonométricas, se obtiene el cos de 82° y se sustituye en la ecuación obtenida:
 |
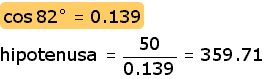Con lo anterior se puede decir que usted se encuentra
a casi 360 metros de la iglesia de Gutiérrez
Zamora. Desde luego, esta distancia es en línea recta desde la
iglesia hasta el lugar al que se movió el observador.
 |
||
 |
 |
 |