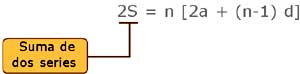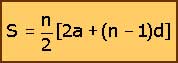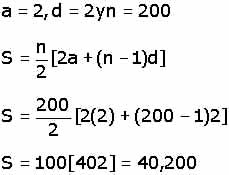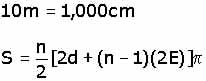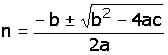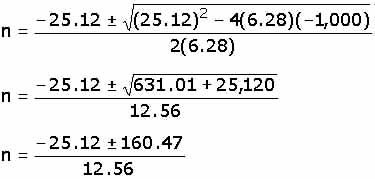Con lo anterior, Marcelo sabe que con un
poco menos de 11 vueltas logrará enredar
toda su cuerda y el diámetro de loscachetes de su carrete será
de 50 cm por lo menos.
Como se puede observar cada vez que se da una vuelta al carrete, su diámetro
aumenta 4 cm debido a que la cuerda mide
2 cm de grueso y así se aumenta el
diámetro en:
A un conjunto de números o literales ordenados de tal manera que
cualquiera de ellos puede ser definido por su antecesor o por el que le
sigue mediante una regla se le llama serie.
En el caso del carrete de Marcelo, la regla es muy sencilla, pues al
analizar los números nos damos cuenta que para conocer qué
sigue de otro, es suficiente con sumarle 4,
o que para conocer el número anterior se logra al restar 4.
Si se observa la tabla que construyó Marcelo, la serie que obtuvo
se puede expresar de la siguiente manera:
S = d, d + [1 (2 E)], d + [2 (2 E)], d + [3 (2 E)]...,
d + [n-1(2 E)]
Cada uno de los elementos de esta serie se llaman términos, y
se simbolizan por la literal "n",
así se tiene que:

Si se observa, "d"
es el diámetro inicial, y la cantidad que se aumenta queda definida
por (n-1) multiplicado dos veces por el grueso
de la cuerda, en este caso, es 2. Así,
cualquier término de la serie estará definido por:
un = d + [(n-1) (2 E)]
Con esta fórmula se puede conocer
cualquier término sin necesidad de tener el anterior o posterior.
Ejemplo
El término 7
de la serie de Marcelo es:
fórmula
de la serie = d + [(n-1) (2 E)] |
sustituyendo, el término 7
será:
10 + [(7-1) (2•2)] = 10 + [6•4]
= 10 + 24 = 34
Con esto, Marcelo ya no tuvo que conocer
los primeros 6 términos para determinar
el 7. Usted puede comprobar lo anterior observando
la tabla de Marcelo.
Así, Marcelo podría conocer
el término 22 de su serie de la siguiente
manera:
d = 10 cm
n = 22
E = 2 cm
|
10 + [(22-1) (2·2)] = 10 + [21·4]
10 + 84 = 94
Esto quiere decir que si Marcelo
da 22 vueltas a su carrete, éste
tendrá un diámetro de 94 cm.
Así con la fórmula que encontró puede calcular
cualquier término de su serie.
|
 |
Para conocer el diámetro de su carrete,
Marcelo necesitó sumar lo que se enredó la cuerda en cada
vuelta. Si no se quiere o no se puede calcular todos los términos
para después sumarlos, se puede utilizar lo que algunos matemáticos
hace siglos encontraron para sumar los términos de una serie.
Observe usted cómo se obtiene una fórmula para sumar los
términos de una serie.
| S = 1, 2, 3, 4, ..., [a+(n-1) d] |
en donde:
S = suma de los términos
a = primer término
d = cantidad que se agrega
n = el número de término |
Esta serie se puede representar de la siguiente manera:
S = a + [a + d] + [a +2d] + [a + 3d] ... + [a + (n -
4) d] + [a + (n - 3)d] + [a + (n - 2)d] + [a + (n - 1)d]
Si se suman dos series pero en una de ellas se inicia
por el último número:
S = a + [a + d] + [a +2d] + [a + 3d] ... + [a + (n -
4)d] + [a + (n - 3)d] + [a + (n - 2)d] + [a + (n - 1)d]
+ S = [a + (n - 1)d] + [a + (n - 2)d] + [a + (n - 3)d]
+ [a + (n - 4)d] ... + [a + 3d] + [a + 2d] + [a + d] + [a]
2S = [2a + (n - 1)d] + [2a + (n - 1)d] +[2a + (n - 1)d]
... + [2a + (n - 1)d] + [2a + (n - 1)d] + [2a + (n - 1)d] + [2a + (n -
1)d]
Se puede ver que todos los
términos son iguales y además que éstos son en número
igual que "n", por lo que se
puede escribir que:
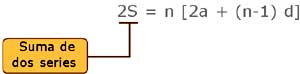
despejando la S,
se tiene:
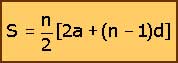
Con esta fórmula se puede obtener la suma de los
términos de una serie. En ella, sus literales significan lo siguiente:
S = suma de la serie
aritmética
n = número de términos
a = primer término
d = cantidad constante que se suma o
se resta |
Ejemplo
Si se quiere conocer la suma de los primeros 200
números pares:
2 + 4 + 6 + 8 + ... n = S
Se tiene que:
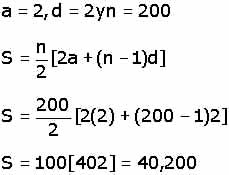
Para saber el último término
(un) de esta serie se tiene:
| un =
a + (n - 1) d
un = 2 + (200 - 1) 2 = 2 + 398 = 400 |
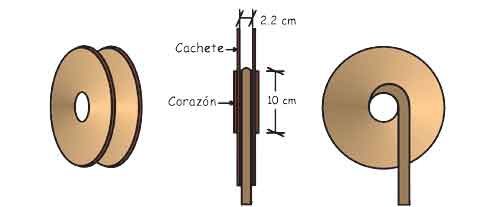
Con estas fórmulas, Marcelo podría ahorrar mucho tiempo
en el cálculo de los cachetes de su carrete. Observe usted cómo
haría sus cálculos.

Como la longitud a enredar de la cuerda es 10 m
y esto se logra al sumar el perímetro de cada vuelta, la suma de
la serie será de:
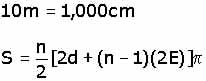
Observe que los términos de la serie se multiplicaron
por 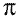 para obtener el perímetro de la cuerda que se enreda con cada vuelta.
En la fórmula se tiene que:
para obtener el perímetro de la cuerda que se enreda con cada vuelta.
En la fórmula se tiene que:
S = 1,000 cm -----------
suma de la serie
n = ? --------------------- número
de vueltas (términos)
d = 10 cm --------------- cantidad de
inicio
E
= 2 cm ---------------- espesor de la cuerda |
Sustituyendo:

Esta ecuación es de segundo grado, por lo que se
puede resolver aplicando la fórmula general:
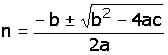
En donde
b = 25.12
a = 6.28
c = - 1,000
|
Sustituyendo
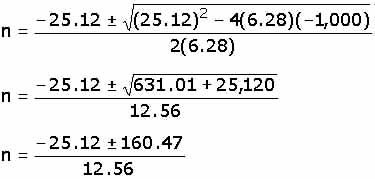
Como en este problema la respuesta sólo puede ser
positiva, se tiene que:
Con lo que se obtiene que con menos de 11
vueltas se enredan los 10 metros de
la cuerda de Marcelo.

Todo lo anterior señalado para las series es para
definir una formula o ecuación que sirva para calcular los términos
de las series y la suma de ellas. No siempre es necesario conocer dichas
fórmulas o ecuaciones, en ocasiones, por sentido común,
se calculan los términos.
En los problemas de matemáticas, las series son muy utilizadas
ya sea para el planteamiento de los problemas o para el planteamiento
de fórmulas que den su solución.
Por lo regular, las series se presentan como un conjunto
de números, todos en orden, y la definición de una regla
o fórmula para calcular los números que van antes o que
siguen se hacen de manera sencilla por medio de la reflexión.
Ejemplos
95, 90, 85, _____ , 75, 70, 65
Como se puede observar, a cada número se le van
restando 5 para definir el siguiente, por
lo que el número que falta es el 80.
68, 75, 82, 89, 96, 103, _____
En esta serie, se van sumando 7
a cada número para conocer el número que sigue, por lo que
el número que falta es el 110.
79, 72, 66, 59, 53, 46, _____
En esta serie, primero se restan 7
al número para obtener el siguiente y luego a ese que se obtuvo
se le restan 6. Observe la solución:
79 - 7 = 72
|
72 - 6 = 66
|
66 - 7 = 59
|
59 - 6 = 53
|
53 - 7 = 46
|
46 - 6 = 40
|
El número que falta es el 40.
128, 64, 32, 16, 8, 4, ______
Observe que en esta serie se divide al número
entre 2 para obtener el siguiente, por lo
que el número que falta es:
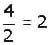
144, 72, 24, 12, 4, ______
En esta serie, primero se divide entre dos
para obtener el siguiente número y ese se divide entre tres. Observe
la secuencia:
144 ÷ 2 = 72 |
72 ÷ 3 = 24
|
24 ÷ 2 = 12
|
12 ÷ 3 = 4
|
4 ÷ 2 = 2
|
El número que falta se obtiene dividiendo a 4
÷ 2 = 2
7, 24, 17, 34, 27, 44, ______
En esta serie, en cada tercer término
se agregan 10. Observe la secuencia:
| 7 + 10 = 17 |
17 + 10 = 27
|
27 + 10 = 37 (Este
número es el que sigue)
|
|
| 24 + 10 = 34 |
34 + 10 = 44
|
Presione el siguiente botón y realice la actividad que se propone.

|

![]() (pi por diámetro), por lo que con cada vuelta que dé la
cuerda, en el carrete enrollará
(pi por diámetro), por lo que con cada vuelta que dé la
cuerda, en el carrete enrollará ![]() longitud,
pero en cada vuelta el diámetro (D)
aumentará 2 veces el espesor (E).
Observe usted:
longitud,
pero en cada vuelta el diámetro (D)
aumentará 2 veces el espesor (E).
Observe usted: