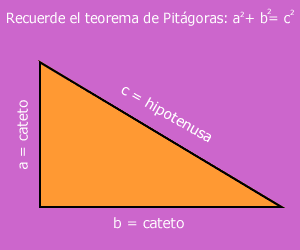
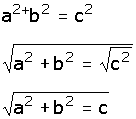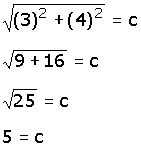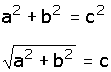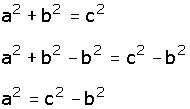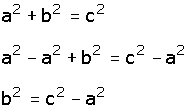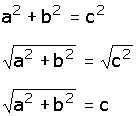Para evitar que un poste de luz se rompa, Rocío debe colocar un cable de acero desde su punta hasta el piso como se muestra en el dibujo.
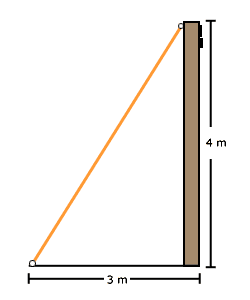 |
El poste mide de altura 4m y el
cable en el piso debe estar separado 3m de la base del poste. Rocío
debe comprar el cable de acero a la medida adecuada, pues no le debe
faltar ni sobrar. ¿Qué
debe hacer Rocío para saber cuánto comprar de cable? |
Rocío piensa que con una escalera y una cuerda puede conocer la
longitud que hay desde la punta del poste hasta el piso a los tres metros
de la base del poste, pero no tiene ni escalera ni cuerda. Entonces piensa
que por medio del teorema de Pitágoras puede solucionar su problema.
Observe lo que hizo:
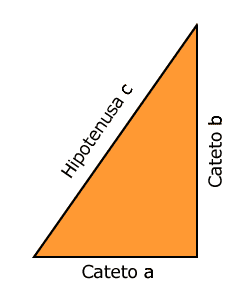
El teorema de Pitágoras dice que la suma del cuadrado de los catetos
es igual al cuadrado de la hipotenusa. Esto significa que: ![]()
 |
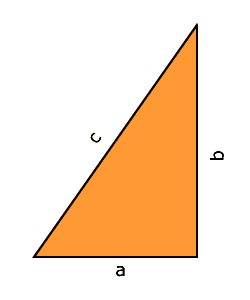 |
Por lo que si Rocío conoce el cateto "b" (la altura del poste) y el cateto "a" (la separación del cable), podrá conocer la hipotenusa "c" (la longitud del cable).
a = 3 m
b = 4 m
c = ?
| Para despejar la "c" (la hipotenusa), se saca raíz cuadrada en ambos miembros de la ecuación.
|
|
Sustituyendo los valores
de a = 3 y
|
Por lo que el cable deberá medir 5 metros más la longitud necesaria para fijarlo al poste y al piso.
Como puede usted ver, el teorema de Pitágoras es muy práctico
para calcular la magnitud de uno de los lados de un triángulo rectángulo,
cuando se conocen sus otros dos lados.
Pero ¿cómo fue que Pitágoras, hace más de 2500 años, encontró esta fórmula tan útil?. hay varias formas de comprobar la fórmula de Pitágoras pero las dos más sencillas son las siguientes.
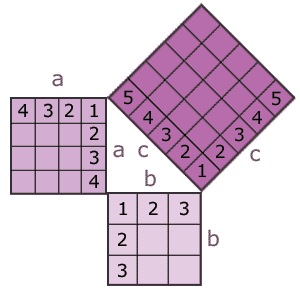
Primero, para ciertos números enteros con 3, 4, 5 llamados triple de Pitágoras.
 |
|
| a=cateto
1 b=cateto 2 c=hipotenusa |
Si se analiza la figura anterior, se tiene que la suma de las áreas de los dos cuadrados que forman los catetos es de:
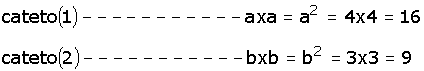
Si se suman las áreas de los cuadrados se tiene:
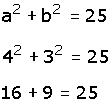
El área del cuadrado que se construye con las dimensiones de la hipotenusa en la figura es de:
![]()
Con lo anterior se comprueba que en un triangulo 3, 4, 5, la suma de los cuadrados de los catetos (a2 + b2) de un triángulo rectángulo (tiene un ángulo de 90°) es igual al cuadrado de la hipotenusa
![]()
Del mismo modo, si multiplicamos otros tres números
(6, 8, 10) por la misma cantidad, obtenemos
otro triple: ![]() e.t.c.
e.t.c.
Segundo, una demostración del teorema de Pitágoras del matemático indio Bashkara, propuesta en el año 1150:
Dos cuadrados, uno dentro del otro. El que está en el interior tiene lados de la magnitud de la hipotenusa de los 4 triángulos rectángulos que se forman con el cuadrado exterior (1) (2) (3) (4).
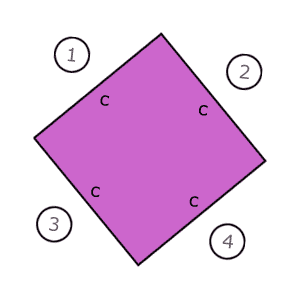
El cuadrado exterior está formado por dos segmentos
(a, b) que son catetos de los cuatro triángulos
formados con el cuadrado interior.
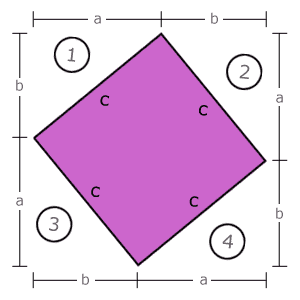
1. Área del cuadrado exterior que tiene lados a + b es:
![]()
2. Área del cuadrado interior que tiene lados c es:
![]()
3. Si se recuerda que el área de un triángulo es igual a la base por la altura entre 2, lo que en los triángulos formados sería( P), y como son 4 triángulos, el área total sería:
![]()
4. Como el área del cuadrado exterior es igual al área del cuadrado interior más el área de los cuatro triángulos, se puede escribir la siguiente ecuación:
Poner la ecuación correcta.
5. Como 2ab se encuentra
en ambos miembros de la ecuación, se puede eliminar:
 |
|
| y queda la ecuación que es el teorema de Pitágoras:
|
|
 |
Recuerda que... El teorema de Pitágoras es aplicable en una gran gama de problemas en los que se conozcan dos de los lados de un triángulo, ya que el otro puede ser fácilmente obtenido al ser despejado, como se muestra a continuación.
|
| a) Cuando se desconoce "c", se saca raíz cuadrada en los dos miembros de la ecuación:
|
|
b) Cuando se desconoce el cateto "a", primero, se resta b2 en ambos miembros y, luego, se saca la raíz cuadrada, también en ambos miembros:
|
c) Cuando no se conoce el cateto "b", se sigue un procedimiento similar al anterior.
| Se resta a2
en ambos miembros:
|
|
Se saca raíz
en ambos miembros:
|
Ejemplos
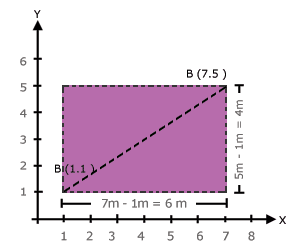
Suponga que tiene una habitación que mide 6 m x 8 m y que en ella hay un tapete bajo muebles muy pesados. Si sólo tiene accesibles dos extremos del tapete, como se muestra en el dibujo, ¿cómo puede usted conocer del tapete la dimensión de cada uno de los lados y su diagonal?

Si las orillas del cuarto se tratan como ejes y cada metro es una coordenada, se tiene que se conocen los puntos A (1, 1) y B (7, 5).
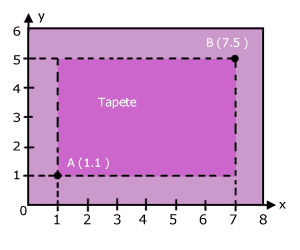
Con lo anterior se pueden calcular las dimensiones de los lados del tapete y con ello la diagonal, que es la hipotenusa del triángulo formado.
|
Observe que con el sistema de ejes coordenados, puede fácilmente obtener las dimensiones de los lados de la figura. Lado paralelo al eje x: Lado paralelo al eje y: |
Para conocer la distancia entre dos puntos cuando sólo se tienen sus coordenadas, se debe recordar que un punto en un sistema de ejes cartesianos (como los que estamos usando) se puede representar por sus coordenadas "x" y "y", así que:
P ( x, y)
A (1, 1)
B (7, 5)
Esto nos indica que la A está en el
punto que se ubica en la x = 1 y la y = 1;
y la B está en el punto en donde la
x=7
y la y = 5.
Si se observan los puntos A y B en el sistema de ejes cartesianos, nos damos cuenta que para obtener la dimensión paralela al eje "x" se restó de la "x2" del punto más alejado del origen (7) la "x1" del punto más cercano al origen (1).
![]()
Y para el lado paralelo al eje "y" se restó a la "y2" del punto más alejado del origen (5) la "y1" del punto más cercano al origen (1).
![]()
Gráficamente esto se puede mostrar de la siguiente manera:
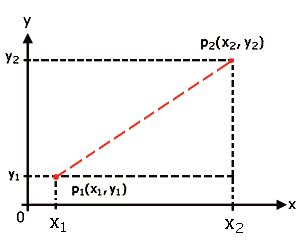
Lo anterior nos permite señalar que la distancia que hay de P1 a N es igual a:
![]()
Y la distancia que hay de P2 a N es igual a:
![]()
En nuestro problema de los muebles si se conocen dos lados del triángulo formado, se podrá, con el teorema de Pitágoras, fácilmente conocer el lado que falta.
Sacando raíz en los dos miembros se tiene que:
Sustituyendo:
Usando la calculadora se tiene que:
|
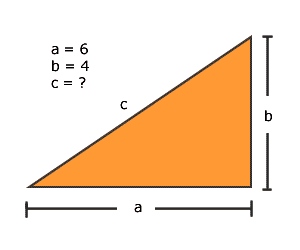
Con lo anterior se puede decir que el tapete tiene un lado de 6 m y otro de 4 m, con una diagonal de 7.21 m.
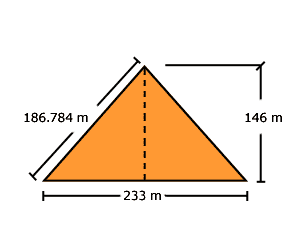
Cuando se descubrió la pirámide Keops de Egipto, fácilmente pudieron medir cuánto medía cada lado de su base (233 m) y la longitud de su pendiente (186.784 m), pero la altura no la midieron físicamente, sino que la calcularon.
¿Cómo calcularía usted la altura de la gran pirámide?
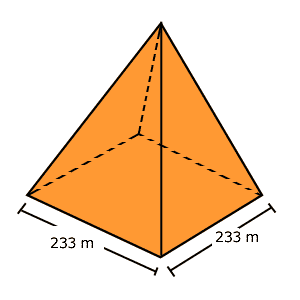
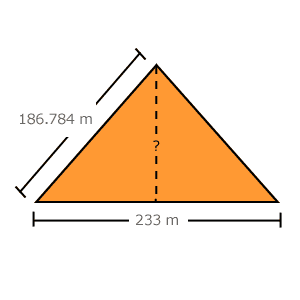
Si observa usted de frente a la pirámide, se dará cuenta que ésta tiene forma de triángulo y que si divide su base a la mitad, se forma un triángulo rectángulo.
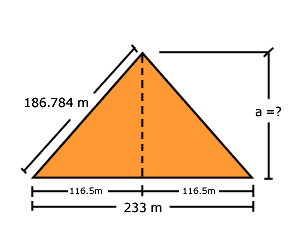
De estos triángulos conoce uno de sus catetos (116.5) y su hipotenusa (186.784), por lo que con el teorema de Pitágoras podrá conocer el cateto que falta. El que es la altura que se está buscando:
Suponga que "a"
es el cateto que se está buscando y que "b"
es la dimensión que ![]() se
conoce de la base. Se despeja "a" restando
b2 en ambos miembros.
se
conoce de la base. Se despeja "a" restando
b2 en ambos miembros.
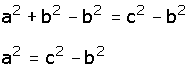
Se saca la raíz cuadrada en ambos miembros.
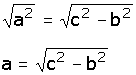
Se sustituyen las dimensiones conocidas:
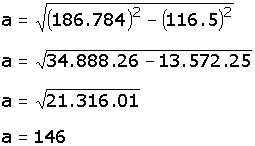 |
|
Con lo anterior se puede decir que la pirámide Keops de Egipto
tiene de altura 146 m.
Presione los siguientes botones y realice las actividades que se proponen.