Tema 2. Multiplicación
A Ramiro, cada año en su trabajo, le proporcionan como prestación el doble de lo que dé la suma de lo ahorrado más intereses a razón del 10% anual.
¿Qué ecuación puede plantear Ramiro para calcular cuánto le deben entregar a fin de año y con ello ayudar a sus compañeros de trabajo a calcular lo que van a recibir?
Pruebe la ecuación que obtenga con lo que ahorrarán las siguientes personas:
| Ramiro | $1,850.00 |
| Juan | $1,125.00 |
| Pedro | $1,420.00 |
| Roberto | $1,560.00 |
Para plantear la ecuación, Ramiro hace lo siguiente:
Va a llamar a la cantidad que ahorra "x" y a la que le van a entregar "y".
Ramiro piensa así: a lo que se ahorra (x) le debo sumar el 10% (0.10) que son los intereses y a ese resultado debo multiplicarlo por 2, porque me dan el doble de lo ahorrado más intereses.
x + 0.1x = cantidad ahorrada más intereses
A la cantidad resultante de lo ahorrado más sus intereses se le debe multiplicar por 2.
2 ( x + 0.1x) = y
Esta es la ecuación que puede utilizar Ramiro. Con ella prueba con sus ahorros, que son $1,850.00, o sea, x = 1,850.
Sustituyendo en la ecuación obtenida, se tiene:
2 (1,850 + 0.1 (1,850) ) = y
Para resolverla hace las operaciones, iniciando por las que están dentro del paréntesis.
2 (1,850 + 185) = |
y |
2 (2,035) = |
y |
4,070 = |
y |
Esto quiere decir que a Ramiro le deben entregar 4,070 pesos de su fondo de ahorro.
Ramiro piensa que para que le sea más fácil ayudar a sus compañeros puede simplificar su ecuación de la siguiente manera.
y = 2 (x + 0.1x)
Como los términos que están dentro del paréntesis son semejantes, los puede sumar con lo que la ecuación quedaría así:
y = 2 (1.1x) |
|
||||||||
Esta ecuación señala que "y" es igual al doble de multiplicar 1.1 por "x".
Para probar, sustituye sus ahorros en la ecuación simplificada.
y = 2 (1.1 (1,850))
Realiza las operaciones.
y = 4,070
Con lo que comprueba que la nueva ecuación está bien planteada y procede a ayudar a sus compañeros. Hace las cuentas con ellos para calcular lo que podrán retirar del fondo de ahorro de cada uno a fin de año.
Ramiro también habría podido simplificar su ecuación de la siguiente manera.
y = 2 (x + 0.1x)
Problema
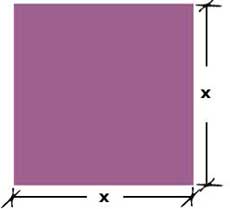
Efraín tiene un terreno cuadrado que mide "x" metros por lado. Ahorra un poco de dinero, y puede comprar 3 metros más de cada lado.
¿Cómo puede Efraín plantear una ecuación para calcular la nueva área de su terreno?
Terreno original
|
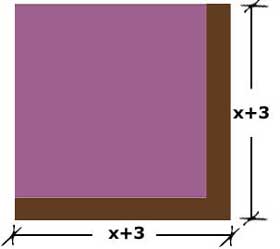
Terreno con 3 metros más por lado
|
Si el área de un cuadrado es lado por lado, A = x · x
El área del terreno original con lados de longitud "x" se determina por la ecuación:
A = x · x = x2
 |
Observe usted que la multiplicación de dos cantidades iguales es lo mismo que elevar esa cantidad al cuadrado. |
En el caso del terreno con 3 metros más en cada lado, su área se puede calcular de la siguiente manera:
A = (x + 3) (x + 3)
Observe que multiplicando por sí misma da (x + 3)2, por lo que se tendrá que:
A = (x + 3) (x + 3) = (x + 3)2
Se
puede realizar la ecuación de manera vertical para obtener su resultado.
Con esto se tiene que:
A = (x + 3)2 = x2+ 6x + 9
Esto quiere decir que para resolver el problema se puede utilizar cualquiera de las dos ecuaciones:
A = (x + 3)2
A = x2 + 6x + 9
Ahora Efraín puede calcular el área de su
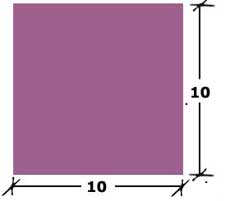
terreno. Para comprobar lo anterior, se puede suponer que el terreno
original tenía 10 m por lado, y probar las dos ecuaciones obtenidas.
terreno original
|
terreno con 3 metros más por lado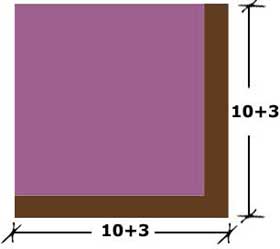 
|
Ahora, aplicando la primera ecuación:
A = (x + 3)2
Sustituyendo x = 10:
A = (10 + 3)2 = (13)2 = 169 m
El área del terreno ampliado es de 169 metros cuadrados.
Ahora, probando la otra ecuación:
A = x2 + 6x + 9
Sustituyendo x = 10:
A |
= |
(10)2 + 6 (10) + 9 |
A |
= |
100 + 60 + 9 |
A |
= |
169 |
Area |
= |
169 m2 |
Ahora suponga usted que Efraín, en lugar de comprar
3 metros más de cada lado, se ve obligado a vender 2 metros en
cada lado. ¿Qué fórmula debe usar Efraín
ahora?
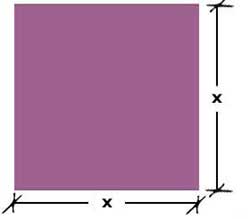
Terreno original
|
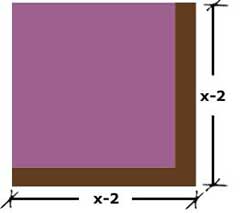
A la dimensión original "x"
se le quitan 2 metros, por lo que cada lado queda de x - 2 |
La fórmula del área de un cuadrado es L x L = L2
El área del terreno reducido se calcula así:
A = (x - 2) (x - 2) = (x - 2)2
Haciendo de manera vertical la operación de (x - 2) (x - 2) se tiene que:
De acuerdo con lo anterior, Efraín puede calcular el área de su terreno reducido 2 m en cada lado, con cualquiera de estas dos ecuaciones:
A |
= |
(x - 2)2 |
A |
= |
x2 - 4x + 4 |
Suponiendo que el terreno original medía 10 m por lado
x = 10
Calculemos un área después de reducirlo en 2 m por lado
 |
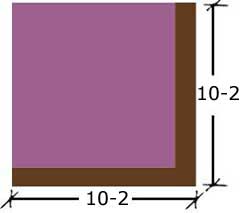A= (x-2)2 A = (8m)2 = 64 m2 |
Ahora, calcularemos el área del terreno reducido utilizando la otra ecuación:
A |
= |
x2 - 4x + 4 |
A |
= |
(10)2 - 4 (10) + 4 |
A |
= |
100 - 40 + 4 = 64 |
A |
= |
64 m2 |
Con lo que se comprueba que la ecuación fue bien obtenida.
Presione el siguiente botón y realice la actividad que se propone.
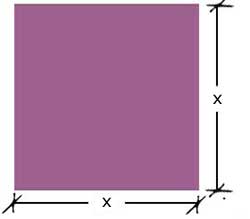
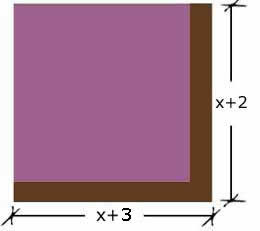
Ahora suponga que Efraín compra 2 m de un lado
de su terreno y en el otro, 3 m. ¿Qué ecuación
utilizaría para obtener el área?
 |
 |
Multimplicando L por L se tendrá:
A = (x + 2)(x + 3)
Si la medida original era 10 m (x = 10), ¿ahora cuál será el área?
Substituyendo x = 10, se tiene:
A = (10)2 + 5 (10) + 6
A = 100 + 50 + 6 = 156
A = 156 m2
Presione el siguiente botón y realice la actividad que se propone.
Algunos productos importantes
Para realizar operaciones (con números o con letras) rápidamente o identificar ecuaciones, existen algunos productos que es conveniente analizar y tener siempre presentes.
Estos productos son:
Estos productos de binomios se les conoce como productos notables, y pueden utilizarse para realizar operaciones fácilmente o simplificar funciones.
Ejemplos
(a +b) (a + b) = (a + b)2 = a2 + 2ab + b2
(a + 3) (a + 3) = (a + 3)2 = a2 + 2a(3) + (3)2 = a2+6a +9
(2a + 3b)2 = 4a2 + 12ab + 9b2
Presione el siguiente botón y realice la actividad que se propone.
 |
||
 |
 |
 |