El
terreno de Jacinto tiene de largo 3 veces lo que mide de ancho. Si al
ponerle una barda alrededor le dicen a Jacinto que ésta mide
400 m, ¿cuáles son las dimensiones de cada uno de sus
lados?
Como Jacinto sabe que su terreno mide de largo 3 veces el ancho, hace un dibujo señalando al ancho con la letra "n".
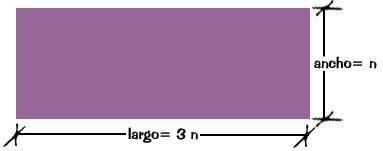
El perímetro de un rectángulo es igual a la suma de las dimensiones de sus lados, por lo que se puede plantear la siguiente ecuación:
n + 3n + n + 3n = Perímetro
Como todos los términos son semejantes (tienen "n") se pueden sumar, por lo que la ecuación se simplifica a lo siguiente:
8 n = Perímetro
Como la barda tiene la longitud del perímetro, se puede escribir la ecuación de la siguiente manera:
| Perímetro = 400 metros |
Para despejar la "n" de la ecuación, se dividen los dos términos entre 8.
8 n |
= |
400 metros |
8 |
8 |
|
|
n = 50 metros
|
||
Por
lo que se puede decir que el ancho (n) del terreno de Jacinto mide 50
m; como el largo mide tres veces el ancho, se sustituye en la ecuación
que da el largo:
3 n |
= |
largo |
3 (50 metros) |
= |
150 metros |
El largo del terreno de Jacinto es de 150 m.
En el problema anterior, se observó que cuando los términos de una ecuación son semejantes éstos se pueden sumar.
Recuerde que
término semejante significa que está constituido
por los mismos elementos que otro. |
En este caso, los términos que tenían un número y una literal (n) se presentaron con un número (o dígito) y una letra (n).
Ejemplo
Una persona corre 24 kilómetros. En los primeros 12 km, tarda 1 hora 5 minutos; los 12 km restantes los hace en 1 hora 12 minutos. ¿Cuánto tardó en recorrer los 24 km?
Observe que en este problema se tienen números y unidades de tiempo.
Para fines de este ejemplo, suponga que las horas las representa por "a" y los minutos por "b". Con esto usted podrá decir que el corredor hizo los siguientes tiempos:
Los primeros 12 km los corrió en 1a 5b y los segundos 12 km los corrió en 1a 12b.
Como sabemos que sólo se pueden sumar términos semejantes (a's con a's y b's con b's), tendremos lo siguiente:
| + |
|
|
|
|
|
Se suman las a's con las a's y las b's con las b's; sustituyendo a = horas y b = minutos, se tendrá:
tiempo en 24 km |
= |
2a + 17b |
tiempo en 24 km |
= |
2h + 17 min |
 |
Recuerde que sólo se pueden sumar o restar números con términos semejantes (manzanas con manzanas, minutos con minutos, horas con horas, a's con a's, etcétera). |
Ejemplos |
|
| a + a = 2a 2a - a = a a - 2a = -a 3x - 2x - x = 0 3y - 0.5y = 2.5y |
3x + 2x - y = 5x - y
12x - 8x - 4x - 6x + 7x = x 12x - 8x - 4x - 6x + 6x = 0 |
w
+ 
wPresione el siguiente botón y realice la actividad que se propone.
Las operaciones algebraicas se pueden realizar de manera vertical u horizontal. En algunas ocasiones, para equivocarse menos o tener mayor orden en la operación, conviene hacerlas de manera vertical.
Sin embargo, por lo regular los resultados de las ecuaciones se presentan siempre en forma horizontal.
Casi todas las operaciones que hemos presentado hasta este momento han estado en forma horizontal por lo que a continuación se presentan algunas operaciones en forma vertical.
Presione el siguiente botón y realice la actividad que se propone.
Los paréntesis en las sumas y restas algebraicas
En algunas ocasiones es necesario indicar qué operaciones se hacen primero que otras, o que si con el resultado de una operación se va ejecutar otra operación.
El signo que va antes del paréntesis es muy importante ya que si son positivos todos términos que están dentro del paréntesis quedan igual, pero si el signo es negativo, para eliminar el paréntesis se deben cambiar todos los signos de los términos que están contenidos en él.
Ejemplos
|
|
||
|
|
Lo anterior se puede observar mejor si se analiza cómo se resuelven las siguientes operaciones algebraicas.
Se requiere sumar "A" más "B - C".
Lo anterior se puede expresar de la siguiente manera:
A + (B - C).
Como el signo que antecede al paréntesis es POSITIVO , lossignos de los términos que se encuentran dentro del paréntesis no cambian si se quita el paréntesis.
A + (B - C) = A + B - C |
Ahora suponga que a la cantidad "A" le va a restar la cantidad
"B - C".
Esto se puede expresar de la siguiente manera:
A - (B - C)
Como el signo que antecede al paréntesis es negativo, todos los elementos que están dentro del paréntesis deben cambiar de signo, al quitar el paréntesis.
A - (B - C) = A - B + C
Ejemplos
2x - (3y + 4z) = 2x - 3y - 4z
7w + (12z - 7x + 4m) = 7w + 12z - 7x + 4m
12n - (14m - 8m) = 12n - 14m + 8n = -14m + 20n
-6a - (4b - 12a + 7c) = 6a - 4b +12a - 7c = 6a - 4b - 7c
Presione el siguiente botón y realice la actividad que se propone.
 |
||
 |
 |
 |