Las divisiones que contengan letras (variables) se pueden realizar cuando el divisor y el dividendo tienen las mismas letras.

Ejemplos

	Todo número dividido entre sí mismo da la unidad.
	Como es la unidad, el resultado de esta operación es -2. Observe que el signo negativo resulta de hacer una división entre cantidades con signos diferentes (+) ÷ (-) = (-)
	Como el ejemplo anterior, cuando en una división el numerador y el denominador tienen la misma literal,ésta se convierte en la unidad, misma que no es necesario señalar.

También se pueden hacer divisiones de términos en donde sólo el divisor o el dividendo tenga una literal.

Ejemplo

¿Cuál será la mitad de -6 °C?

En este caso, los grados centígrados se pueden considerar como una literal, o sea que lo anterior se observaría también en la siguiente operación.

Ejemplos

Observe en el último ejemplo que cuando una literal está en el denominador y se desea poner en el numerador se puede subir con su exponente (en este caso, 1), pero se sube con signo negativo (4^-1).

Cuando se multiplican varias letras por sí mismas adquieren un exponente, este exponente es el número de veces que se multiplica la letra; y se coloca en la parte superior derecha de la letra.

Ejemplo

a · a · a · a · a = a⁵ (indica que se multiplica cinco veces a la "a".)

a⁵ se lee: "a" a la quinta potencia

Piense que cada una de las "a" que se multiplicaron por sí mismas tienen exponente 1 y que cuando se multiplican por sí mismas se suman estos exponentes.

a¹· a¹ · a¹ · a¹ · a¹ = a^(1+1+1+1+1) = a⁵

Si se tuviera una "a²" y una "a", el producto de estas dos literales sería:

a² · a¹ = a⁽²⁺¹⁾ = a³

Ahora, si tuviera una división de "a²" entre "a", se obtendría lo siguiente:

Una de las "a¹" de arriba se elimina con la "a¹"de abajo

o sea que: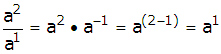

Lo anterior se puede representar de la siguiente manera:

am·an = a(m+n)	En el caso de una multiplicación se suman los exponentes.
	En el caso de una división, se restan los exponentes.

Así, cuando se tiene:

a² · a³ = a⁽²⁺³⁾ = a⁵

O cuando se tiene:

Lo anterior es fácilmente comprobable si se hace lo siguiente:

a3 = a · a · a
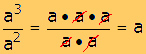a2= a · a

También podría suceder que se tenga una operación en la que el denominador tiene un exponente mayor que el numerador, y lo que se obtiene sería una literal o base con un exponente negativo.

Ejemplo

Si se divide "a²" entre "a⁶", se tendría:

Lo anterior se puede comprobar de la siguiente manera:

Ejemplos

Observe que b0 = 1

La última operación se puede comprobar de la siguiente manera:

Ejemplos

Presione el siguiente botón y realice la actividad que se propone.

Con la misma regla que se realizan las divisiones de los monomios se hacen las de los polinomios.

Ejemplos

Presione el siguiente botón y realice la actividad que se propone.