Tema 3 Planteamiento
de ecuaciones
Amaro tiene tres recipientes
con las siguientes dimensiones.
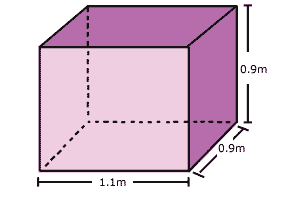 |
| Recipiente 1 |
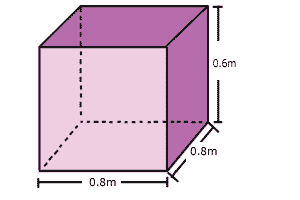 |
| Recipiente 2 |
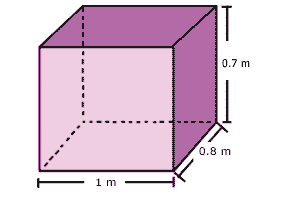 |
| Recipiente 3 |
Para conocer el volumen o capacidad del recipiente 1,
se multiplica el lado del frente del recipiente (1.1
m) por el lado de fondo (0.9 m) por
el alto (0.9 m); de lo anterior se obtiene
lo siguiente:
(1.1 m)
• (0.9 m) • (0.9 m) = (0.891 m3 )
Observe que el signo de multiplicación x (cruz) fue cambiado por un punto para no confundirlo con una letra x (equis). Además, las cantidades de cada lado se colocaron dentro de un paréntesis, lo que nos indica que la m de metros pertenece al número que acompaña.
De la misma manera se puede calcular el recipiente 2: frente (0.8m) por su fondo (0.7m) por su alto (0.6m).
(0.8 m)•(0.7 m)•(0.6 m) =
0.336 m3
 |
Recuerde
que m • m • m = m3 |
También en el tercer recipiente hacemos lo mismo: frente (1 m) por fondo (0.8 m) por alto (0.7 m).
(1 m)•(0.8 m)•(0.7 m) = 0.56 m3
 |
Recuerde que el signo de multiplicación (x) puede ser cambiado por un punto para no confundirlo con una letra x (equis). |
Para conocer el volumen de los tres recipientes, se multiplicó la dimensión del frente por la del fondo y por la de la altura.
Si al frente se le llama "a", al fondo "b" y a la altura "h", tendremos que el volumen (V) se obtiene de la siguiente manera.
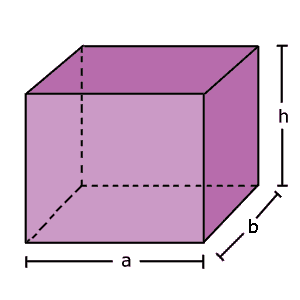 |
V = a • b •h |
En esta ecuación, las letras "a", "b" y "h" pueden adquirir cualquier valor del frente, fondo y alto de un recipiente. Por lo que se puede decir que esta fórmula sirve para calcular el volumen de cualquier paralelepípedo regular.
A las expresiones como la anterior en donde sus componentes son letras que se suman, restan, multiplican o dividen se les llaman expresiones algebraicas y se utilizan mucho para expresar fórmulas o para indicar las operaciones que debemos seguir para obtener un resultado.
Uso |
Enunciado |
Expresión
algebraica |
| Área de un rectángulo |
Área
= (base) x (altura) |
A = b •
h |
| Área de un triángulo |
|
|
| Perímetro de un círculo |
Perímetro
= ( |
p= (constante) |
| Volumen de un cilindro |
Volumen = (área de la base) x (altura) (área de la base) = |
V = psi • r2 • h (constante) |
| Volumen de un cono |
Volumen = (área de la base) x (altura) (área de la base) = |
(constante) |
| Presión |
|
|
| Velocidad |
|
|
| Voltaje |
Voltaje = (resistencia) x (corriente)
|
V = R • I |
 |
Recuerde que |
Con el álgebra se pueden simplificar las expresiones algebraicas ya que las letras pueden tener cualquier valor.
Ejemplo
Si se conoce que el área de un rectángulo es el producto de multiplicar su base (b) por su altura (h), tenemos que:
|
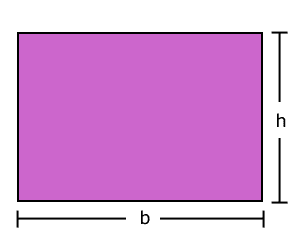 |
Si a ese rectángulo le trazamos una línea
diagonal y lo dividimos en dos partes, tendremos dos triángulos.
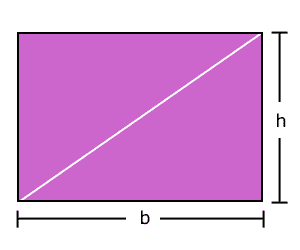 |
Con lo anterior, podemos señalar
que el área de un triángulo es igual a la de un rectángulo,
pero dividido entre dos.
Área de un
triángulo = |
|
Como el área de un rectángulo es igual a multiplicar la base por la altura:
A = b • h
se puede construir una expresión algebraica que nos indique cuál es la fórmula para obtener el área de un triángulo.
Con las expresiones algebraicas se pueden plantear ecuaciones numéricas para resolver problemas en la vida cotidiana.
Ejemplo
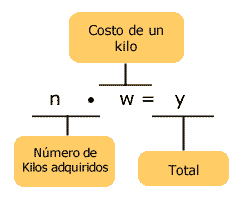
Si el costo de un kilo de plátanos es "w" pesos, ¿cuál será el costo total "y" de "n" kilos de plátanos?
Planteamiento de la ecuación:
El costo de un kilo de plátanos es igual a "w". Si se adquieren "n" kilos de plátanos, el total "y" será igual a multiplicar lo que cuesta un kilo (w) por el número de kilos que se adquieran (n).
| Por lo que la ecuación
será la siguiente:
|
|
En algunas ocasiones, no se coloca el punto para indicar la multiplicación, por lo que la ecuación anterior también podría ser expresada de la siguiente manera:
|
Ejemplo
Si Malena en el mercado compra "n" kilos de plátano y el kilo cuesta "w" pesos, ¿cuánto tendrá que pagar al frutero si éste le debe 8 pesos de cambio?
Planteamiento de la ecuación:
"n" kilos de plátano por "w" pesos que cuesta cada kilo sería el total; pero como le deben a Malena 8 pesos, se debe restar 8 al producto de "n" por "w".
Por lo que la ecuación quedará de
la siguiente manera:
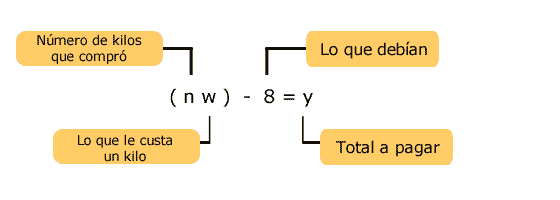
Observe que para indicar que primero se multiplica el número de kilos por lo que cuesta un kilo, esto fue encerrado en un paréntesis y, luego, se le restan los 8 pesos que le deben a Malena.
Si esto no se hace, puede haber confusiones, porque no se sabría si se le quitan los 8 pesos a la "w", lo que es incorrecto porque no es lo mismo multiplicar "n" por "w" y al producto quitarle los 8, que quitarle 8 a "w" y lo que dé multiplicarlo por "n".

Observe qué pasa si el kilo de plátanos cuesta 4.50 pesos y Malena compra 4 kilos.
| Con la ecuación bien planteada: (n • w) - 8 = y
(4 • 4.50) - 8 = y (18) - 8 = y 10 = y Malena debe pagar sólo 10 pesos. |
|
Con la ecuación
mal planteada: n • w - 8 = y Aquí no se sabe si primero restar a "w" 8, o primero multiplicar "n" por "w" y, luego, restar. Observe qué pasa si primero a "w" se restan 8. 4 • 4.50 - 8 = y 4 • (-3.50) = y -14 = y Lo que es diferente a lo que debe pagar Malena. |
Cuando en una ecuación hay varios términos con los que se
hacen productos o divisiones, se agregan o restan cantidades, es muy importante
señalar con paréntesis qué se multiplica o divide,
qué se resta o suma.
Ejemplo
Ernesto va a comprar "n" litros de pintura vinílica blanca. Como es buen cliente, en el precio de cada litro ("b" pesos), le hacen un descuento del 10% (0.1 b). ¿Cuál será la ecuación con la que puede calcular lo que debe pagar si compra diferentes cantidades de pintura de diferentes precios?
Pruebe su ecuación para cuando Ernesto compra lo siguiente:
a) 5 litros de pintura de
13 pesos cada litro
b) 14 litros de pintura de 18
pesos cada litro
c) 3 litros de pintura de
7 pesos cada litro
| Planteamiento de la ecuación: Costo de un litro con descuento: b - (0.1 b) Costo de "n" litros con descuento:
en donde: n = número de litros que va a comprar |
|
|
Observe que se asignó la letra "y" al costo total con el descuento. Podría haber sido cualquier letra. También observe que hay un paréntesis (0.1 b) dentro de otro paréntesis (b - (0.1 b)).
| a) Prueba de la ecuación
Sustituyendo "n" y "b" en la ecuación: y = 5 (13 - (0.1 • 13)) Primero, se multiplica el (0.1 • 13) para quitar el paréntesis que está dentro del paréntesis: y = 5 (13 -(0.1 • 13)) y = 5 (13 - 1.3) Luego, se hacen las operaciones que están en el paréntesis que queda, para ser eliminado. y = 5 • 11.7
y = 58.50 Debe pagar 58.50 pesos.
|
|
b) Prueba de la ecuación
Sustituyendo:
Se hacen las operaciones del paréntesis que está dentro del otro paréntesis para que sea eliminado. y = 14 (18 - 1.8)
Se elimina el paréntesis que queda, haciendo las operaciones de los números que están en él. y = 14 • 16.2 y = 226.80
Debe pagar 226.80 pesos.
|
Presione el siguiente botón y realice la actividad que se propone.
La ecuación se diseñó para que Ernesto sepa cuánto pagar con descuento por su pintura:
y = n (b - 0.1 b)
Pero puede ser simplificada ya que el término (b
- 0.1 b) es igual a (0.9 b), porque:
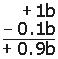 |
Esto se puede hacer porque los dos términos tienen
"b".
Por lo anterior, se puede simplificar aún más nuestra ecuación, de la siguiente manera:
y = (0.9 b) n
Para comprobar que esta ecuación es lo mismo que la que antes se había obtenido, la probaremos con los datos:
| a) n = 5, b = 13 b) n = 14, b = 18 c) n = 3, b = 7 |
a) Sustituyendo cuando n
= 5 y b = 13, se tiene:
| y = (0.9 b) n y = 0.9 (13 • 5) y = 0.9 (65) y = 58.5 |
Cantidad igual a la que se obtuvo con la ecuación anterior.
Presione el siguiente botón y realice la actividad que se propone.
Como se puede observar, con las letras se
pueden hacer operaciones, con lo que las ecuaciones algebraicas se pueden
simplificar y facilitar los cálculos. En la próxima unidad,
usted aprenderá a hacer operaciones con las letras y a simplificar
las operaciones.
Presione el siguiente botón y realice la actividad que se propone.