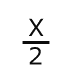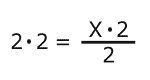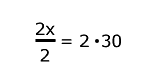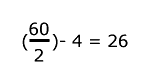Las igualdades también se llaman ecuaciones;
siempre están compuestas de dos lados o miembros y entre ambos
existe un signo de igualdad.
|
Elementos del primer miembro |
|
Elementos del segundo miembro |
Ejemplo
|
3 x 6 |
|
6 + 6 + 6 |
|
|
Primer miembro |
Segundo miembro |
|
( 6 ÷ 2 ) x 3 |
|
( 3 x 3 ) ÷ 1 |
|
Primer miembro |
Segundo miembro |
A los elementos
que componen un miembro, se les llama términos.
Cuando no se conoce uno de los términos o elementos de los miembros de una ecuación, a éste se le conoce como incógnita y se puede representar por una letra (por ejemplo, la "x" ).
 |
Recuerde que para que la "x" no se confunda con el signo de multiplicación ( "x" ) en lugar de éste se usa " un punto " o se ponen las cantidades entre paréntesis. |
Ejemplo
|
3 x 6 = 8 + 8 + |
x |
En esta igualdad hay una incógnita, la que representamos como "x".
Para conocer una incógnita "x",
se recomienda realizar
primero todas las operaciones posibles en la ecuación para hacerla
lo más simple posible.
Observe cómo
se puede obtener el valor de "x" en la
ecuación anterior.
Para que el signo de multiplicación (x) no se confunda con la incógnita, se usará a partir de ahora un punto (•) o paréntesis como signo de multiplicar.
¿Cuánto vale x?
| 3•6 = 8 + 8 + x | |
| (3) (6) = 8 + 8 + x | |
| 18 = 16 + x |
Para dejar sola a la "x" en el segundo miembro de la ecuación, debo quitarle (restar) 16, porque al valor de la "x" se le está sumando 16.
segundo término: 16 + x - 16
Como resté 16 en el segundo miembro, para que se conserve la igualdad, también debo restar en el primero:
|
 |
 |
No olvide que para conservar una igualdad, lo que suma o resta en un miembro de la ecuación lo debe sumar o restar en el otro. |
Ejemplo
¿Cuál es el valor de la incógnita en la siguiente ecuación?
Ecuación original:
12 + 25 - 2 = 13 - 3 + 15 + x
Paso 1
Simplificar al máximo la ecuación.
12 + 25 - 2 = 13 - 3 + 15 + x
35 = 25 + x
|
Paso 2 En este caso, para que quede sola, hay que restarle
25 en el 2° miembro y para que la igualdad se mantenga, también
se deben restar en el primer miembro. 35 - 25 = 25 + x - 25 |
|
Paso 3 35 - 25 = 25 - 25 + x
El valor de"x"es igual a
10. |
Para comprobar que no hay equivocaciones,
podemos
poner el valor de "x", que obtuvimos, en la ecuación
original.
Ecuación original:
12 + 25 - 2 = 13 - 3 + 15 + |
X |
Se sustituye a la "x" (la incógnita) por el valor que se encontró (10).
12 + 25 - 2 = 13
- 3 + 15 + |
( 10 ) |
Se resuelven las operaciones indicadas.
35 = 35
Se comprueba que, cuando "x" tiene el valor de 10, la ecuación se satisface.
Ejemplo
Paso 3
| Ecuación original 15 - (3 • 2) = 3 • x Paso 1
15 - 6 = 3 • x 9 = 3 • x |
|
Paso 2 9 = 3 • x En este caso, para despejar a la incógnita, se debe dividir al segundo miembro entre tres, y para que la igualdad se mantenga, también el primer miembro se debe dividir entre tres.
|
Se resuelven las operaciones para obtener el valor de la incógnita.
 |

|
Recuerde que cualquier número multiplicado por 1 resulta el número original. |
|
3 = 1 • x |

|
Observe que no es necesario poner el número 1 antes de una letra. |
El valor de x es 3.
Para comprobar si el valor obtenido de la incógnita es adecuado, se sustituye éste en la ecuación original.
15
- (3 • 2) = 3 • |
X |
15 - (3 •
2) = 3 • |
(
3 ) |
| 15 - 6 = 9 |
|
| 9 = 9 |
La igualdad se comprueba, por lo que la solución es adecuada.
Ejemplo
|
Paso 1
Simplificar al máximo la ecuación, resolviendo las operaciones que sean posibles.
(Primero se resuelven las operaciones de los números que están dentro del paréntesis.)
|
|||
|
|||
|
|
Paso 2 En este caso, como la "x" está dividida entre 2, para que quede sola ésta se debe multiplicar por dos. Y para que la igualdad no se altere, se debe también multiplicar al primer miembro por dos.
|
|
Paso 3
|
El valor de "x" en la ecuación es 4 ó, lo que es lo mismo,la ecuación se resuelve cuando "x" tiene el valor de 4.
Para comprobar que lo anterior es verdadero, se sustituye el valor obtenido en lugar de la incógnita y se realizan las operaciones.
| -
14 + (20 - 4) = |
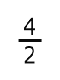 |
-14
+ 16 = |
2 |
2 = |
2 |
Se cumple la igualdad. |
Ejemplo
Ecuación original:
5 - (x - 1) = 10
Paso 1
Se resuelve en lo posible la ecuación, ejecutando las operaciones.
5 - (x - 1) = 10
Observe que para ejecutar las operaciones, es necesario quitar el paréntesis que está precedido por un signo negativo, lo que significa que cada uno de los signos de los componentes del paréntesis deben ser multiplicados por (-).
Como la "x" no tiene un signo escrito quiere decir que tiene signo positivo (+) y como (-) por (+) da menos, entonces, al eliminar el paréntesis, la "x" queda con signo negativo.
Aún falta sacar del paréntesis al -1; como el signo que está fuera del paréntesis es (-) y el del 1 es también (-),entonces (-) por (-) es igual a (+) por lo que el uno tendrá signo positivo.
5 - x + 1 = 10
|
| - x + 6 = 10
|
Paso 2
Se despeja la "x". Para ello se resta el 6 en los dos miembros
de la ecuación, quedando así:
- 6 + 6 - x = 10 - 6
|
0 - x = 4 |
Presione el siguiente botón y realice la actividad que se propone.
Las ecuaciones sirven para plantear las soluciones a problemas en los que falta un dato, como se observa a continuación.
Marcela compró 5 tazas. Si por ellas pagó 25 pesos, ¿cuánto costó cada taza?
|
Paso 1 5 • x pesos = 25 pesos |
|
Paso 2 En este caso, la ecuación está simplificada ya que todas las operaciones ya fueron ejecutadas. 5 • x pesos = 25 pesos |
Tratar de dejar sólo una taza (que es el valor que se busca); para esto, se deben de dividir entre 5 a los dos miembros de la ecuación.
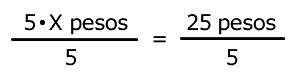 |
Paso 3
| Se ejecutan las operaciones, y se tiene que: | 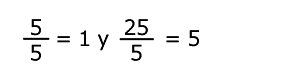 |
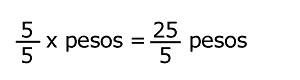 |
| 1•x pesos = 5 pesos |
| x = 5 |
|
Lo que significa que cada taza tiene un valor de 5 pesos |
Ejemplo
La señora Olivia cobró a un cliente 27 pesos
por 5 litros
de leche y una barra de mantequilla que vale 3 pesos.
¿Cuánto cuesta cada litro de leche?
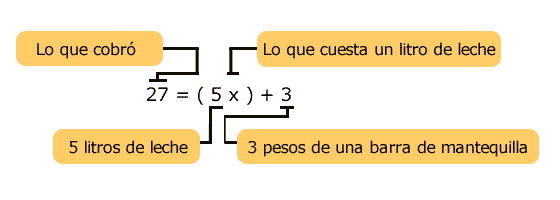
Observe que ya no se puso el punto para indicar (5 • x).
Es importante saber que aun cuando se acepta escribir 5x+3, en este ejemplo se puso un paréntesis al (5x) para evitar la confusión de si primero se le suma a la "x" el 3 y luego se multiplica por, lo que es incorrecto, ya que algebraicamente eso se escribiría así: 5 (x+3).
Se deja sola a la "x".
Para quitar el +3, se restan 3 en los dos miembros.
27 - 3 = (5x) + 3 -3
24 = 5x
Luego, para quitar el 5
que está multiplicando a la "x",
se divide entre 5 a los dos miembros.
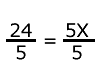 |
4.80 = 1x
De acuerdo con lo anterior, cada litro de
leche (x)
cuesta 4.80 pesos.
Para comprobar lo anterior, se sustituye
el valor de
x = 4.80 en la ecuación original.
27 = 5x + 3
27 = (5 • 4.80) + 3 (Aquí se
usó el punto para evitar confusión.)
27 = 24 + 3
27 = 27
Se cumple la igualdad, por lo que la ecuación
numérica fue bien resuelta.
Ejemplo
Humberto vendió
4 toneladas de maíz; después de haber
pagado 100 pesos de impuestos, le quedaron 2,500 pesos.
¿En cuánto vendió cada tonelada de maíz?
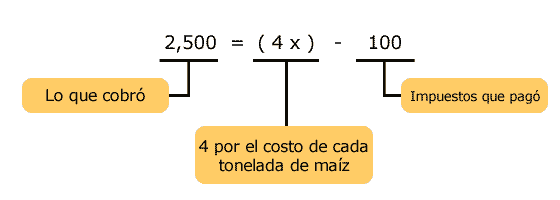
Para resolver la ecuación, se deja sola a la "x" (la que no se conoce).
|
Para eliminar el -100 en el segundo miembro, se suman 100 en los dos miembros. 2,500+100= 4x-100+100 Se ejecutan las operaciones y nos queda: 2,600 = 4 x |
 |
Para quitar el 4 que está multiplicando a la "x", se dividen los dos miembros entre 4.
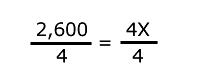 |
|
| |
|
Para comprobar que la ecuación fue bien resuelta, se sustituye el valor de la "x" obtenido en la ecuación original.
|
2,500 = 4 (650) - 100 2,500 = 2,600 - 100 2,500 = 2,500 |
Como se cumple la igualdad, la ecuación fue bien planteada y resuelta.
Ejemplo
Lucrecia tiene 2 hijos. La suma de sus edades es 12 años. Si el más grande tiene 8 años, ¿cuántos años tendrá el menor? Planteamiento de la ecuación: |
 |
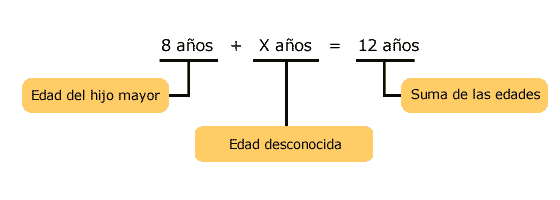
Se despeja a la "x" (edad desconocida); para ello se debe eliminar al 8 que tiene signo positivo, lo que se logra restando 8 en ambos miembros.
8 - 8 + x = 12 - 8 x = 4 |
Lo que nos indica que la edad del hijo pequeño de Lucrecia es de 4 años.
Para comprobar si la ecuación fue bien resuelta, se sustituye el valor de "x" obtenido en la ecuación original.
8 +(4)=12 12 = 12 |
Como la igualdad se cumple, la ecuación está bien resuelta.
Ejemplo
|
Un camión cargado pesa 9,485kg. Si el camión sin carga pesa 1,430kg, ¿cuál es el peso de la carga del camión? Como el peso total del camión con carga debe ser igual al
peso del camión más el peso de la carga, se puede
plantear la siguiente ecuación: |
 |
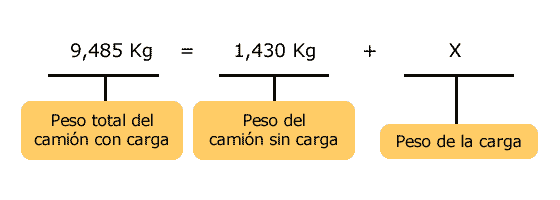
Para dejar sola a la incógnita "x" (lo
que no se conoce),
los 1,430 kg que se están sumando
en el segundo miembro se eliminan al restarles 1,430kg;
pero para que la ecuación no se altere, se deben restar también
en el primer miembro.
9,485kg - 1,430kg = 1,430kg - 1,430kg + x
Al realizar las operaciones se tiene que:
8,055kg = x
Por lo que se puede afirmar que la carga del camión es de 8,055kg.Para comprobar que la ecuación fue bien resuelta,se sustituye el valor obtenido de "x" en la ecuación original.
9,485kg = 1,430kg + (8,055 kg)
9,485kg = 9,485 kg
Como la igualdad se comprueba, la ecuación fue bien resuelta.
Ejemplo
Martín compró un automóvil a crédito, por el que va a pagar en total 87,000 pesos. Si de enganche pagó 26,280 pesos y le quedan letras de 2,530 pesos mensuales,¿en cuántos meses terminará de pagar su auto?
Como lo que cuesta el automóvil menos el enganche debe ser igual a lo que va a pagar al mes por el número de meses, se puede plantear la siguiente ecuación:
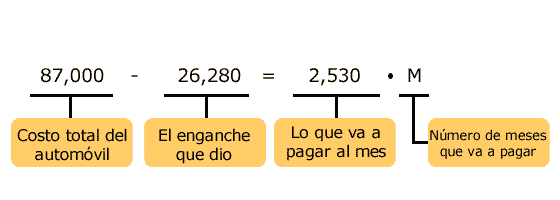
Se resuelven las operaciones de la ecuación.
60,720 = 2,530 • M
Se despeja la incógnita
En este caso, es el número de meses (M) en los que pagará lo que quedó a deber.
Para quitar los 2,530 pesos que están multiplicando a "M"en el segundo miembro, se divide entre 2,530, pero para que no se altere la ecuación, el primer miembro también debe ser dividido entre 2,530.
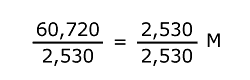 |
Haciendo las operaciones se tiene:
24 = M
Lo anterior indica que Martín pagará su
deuda en 24 meses.
Para saber si se resolvió bien la ecuación, se sustituye
el valor de "M" (24) en la ecuación
original.
87,000 - 26,280 = 2,530 (24)
60,720 = 60,720
La igualdad se comprueba, por lo que la ecuación está bien resuelta.
Ejemplo
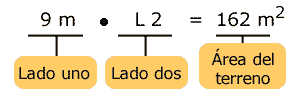
El terreno de la casa de Matías es
rectangular. Si de superficie mide 162 m2
y uno de sus lados tiene 9m,
¿cuánto mide el otro lado?
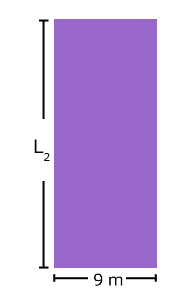 |
Planteamiento de la ecuación: Se sabe que el área de un rectángulo es el producto de sus lados. Por lo tanto, se tiene
que multiplicar el lado 1 (9 m)
por el lado 2 (L2 )
y esto es igual al área del terreno.
|
Para despejar "L2" (la incógnita), se dividen los dos miembros entre 9.
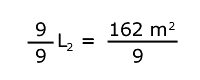 |
| L2 = 18 m |
Se obtiene que el otro lado del terreno de la casa de Matías mide 18 m.
Para comprobar que la ecuación fue bien resuelta, se sustituye el valor de "L2" obtenido en la ecuación original.
9 m • L2 = 162 m2 9 m • 18 m = 162 m2 162 m2 = 162 m2 |
Como la igualdad se comprueba, la ecuación
está bien resuelta.
Ejemplo
Si al número 12 se le agrega 3 veces un número y el resultado es el número 24, ¿cuál es el número que se agregó?
 |
Para quitar los 12 que están sumando,
se restan 12 en ambos miembros.
12 - 12 + (3x) = 24 - 12 3x = 12 |
Para dejar sola a la "x", se dividen
ambos miembros
entre 3.
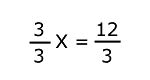 |
x = 4 |
El número buscado es 4. Para comprobar que la ecuación fue bien resuelta, se sustituye el 4 en la ecuación original.
12 + 3 x = 24 12 + 3 (4) = 24 |
La igualdad se comprueba, por lo que la ecuación fue bien resuelta.
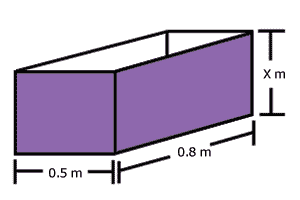
Ejemplo
El ancho y largo de una caja son 0.5
m y 0.8 m, respectivamente. Si su
capacidad es de 0.4 m3,
¿cuál es la medida del fondo de la caja?
| Como la capacidad de un paralelepípedo es el producto de sus tres lados, se puede plantear la ecuación siguiente:
|
 |
Para dejar sola a la incógnita, primero se resuelven las operaciones de la ecuación.
0.5 m • 0.8 m • x m = 0.4 m 0.4 m • x m = 0.4 m |
Se dividen ambos miembros entre 0.4 y se obtiene:
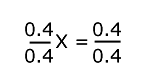 |
x = 1 |
Lo que indica que de fondo la caja tiene un metro.
Para comprobar lo anterior, se sustituye el valor obtenido en la ecuación original.
0.5 • 0.8 • x = 0.4 0.5 • 0.8 • (1) = 0.4 0.4 = 0.4 |
Como la igualdad se confirma, la ecuación estuvo
bien resuelta.
Ejemplo
Pancracio ahorra "x" cantidad de dinero durante un año.
El banco en donde tiene su dinero le da el 11%
de interés. Si se suman 228 pesos
a lo que el banco le dio de interés, se obtienen 580
pesos. ¿Cuánto ahorró Pancracio?
|
Considerando que el 11% equivale a 0.11 de la cantidad ahorrada, ahora se plantea la ecuación:
|
 |
|
Para despejar la incógnita, (0.11x)+ 228-228 =580-228 |
|
Después, se dividen los dos miembros entre 0.11. x = 3,200
|
Con lo anterior se sabe que la cantidad que ahorró Pancracio fue de 3,200 pesos. Para comprobarlo, se sustituye el valor obtenido en la ecuación original.
(0.11) (x) + 228 = 580
(0.11) (3,200) + 228 = 580 352 + 228 = 580 580 = 580 |
Demostrando la igualdad de la ecuación
se confirma que estuvo bien resuelta.
Ejemplo
Si a la mitad de un número se le restan 4 y se obtiene 26, ¿cuál es el número que fue dividido a la mitad?
Planteamiento de la ecuación:
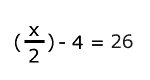 |
Para despejar la incógnita, se suman 4 en los dos miembros de la ecuación.
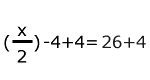 |
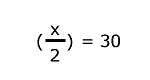 |
|
Y para conocer el valor de "x", se multiplica por 2 a los dos miembros.
|
|
Con lo que el número buscado es 60; para comprobar que la ecuación fue bien resuelta, se sustituye este número en la ecuación original.
|
Se comprueba la igualdad, por lo que la ecuación fue bien resuelta.
Presione el siguiente botón y realice la actividad que se propone.