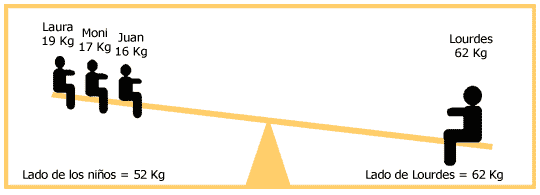
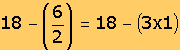Para analizar porqué siempre gana Lourdes, se puede hacer un diagrama como el siguiente.
Como se puede observar, del lado de los niños, hay 19kg + 17kg + 16kg = 52kg.
 |
 |
Para que el sube y baja quede equilibrado, el peso sumado de los tres niños que están sentados al lado izquierdo debería ser igual al de Lourdes, quien está sentada en el lado derecho.
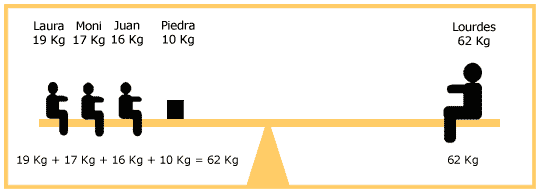
Para que lo anterior suceda, entre los tres niños deberían aumentar el peso 10kg, porque 52kg + 10kg = 62kg (peso de Lourdes).
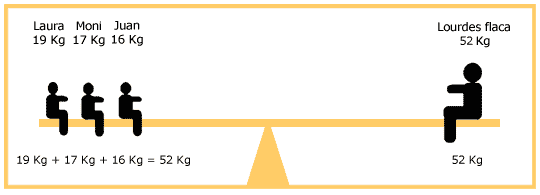
También podría ser que Lourdes adelgace 10 kg y con ello el sube y baja queda equilibrado.
Cuando el peso de un lado se iguala al del otro lado,
el sube y baja se encuentra en equilibrio porque ambos pesos son iguales.
| Peso de los niños más la piedra |
= |
Peso de Lourdes
|
||
| 52
kg + 10 kg |
= |
62 kg | ||
|
= |
|
También podría ser que Lourdes adelgace.
| Peso de los niños |
= |
Peso de Lourdes menos lo que adelgazó
|
||
| 52
kg |
= |
62 kg - 10 Kg | ||
|
= |
|
Cuando los niños no cargan la piedra de 10kg o si Lourdes no adelgaza, el sube y baja estará desigual, o sea, con un lado más pesado que otro, lo que genera que el lado más pesado baje más que el ligero. Esto se expresa de la siguiente manera:
 |
Se dice que hay una desigualdad.
Cuando en los dos lados del sube y baja hay el mismo peso (62kg ó 52kg), se dice que hay una igualdad y se expresa de la siguiente manera.
|
Lado izquierdo: peso de los niños + piedra |
= |
Lado derecho: peso de Lourdes |
||
|
= |
|
| Lado izquierdo: peso de los niños |
= |
Lado derecho: peso de Lourdes flaca |
||
|
= |
|
En ambos casos, el sube y baja estará en equilibrio (ni sube ni baja).
Para que una igualdad (62kg = 62kg) se mantenga como tal, si se agrega o quita algo de un lado, también se debe agregar o quitar del otro.
Ejemplos
|
40 = 40 igualdad |
|
52 = 52 igualdad |
||
|
|
|||
| 30 = 30 también es igualdad | 42 = 42 también es igualdad |
De la misma manera, para que se conserve la igualdad, si en uno de sus lados (también llamado miembro) se multiplica o divide, también se debe multiplicar o dividir por la misma cantidad.
Ejemplos
| 52 = 52 igualdad |
|
52 = 52 igualdad |
||
| Si se multiplica
por 2, se tiene: |
Si se divide entre 2, se tiene: | |||
|
|
|||
| 104
= 104 también es igualdad |
26 = 26
también es igualdad |
Observe que para que una igualdad se conserve como tal, lo que se agregue o se quite en un miembro se debe agregar o quitar en el otro.
Ejemplos
|
 |
Presione el siguiente botón y realice la actividad que se propone.
 |
||
 |
 |
 |