Para hacer más fácil el manejo de las operaciones algebraicas, se recomienda conocer algunas definiciones para que al referirse a ellas se entienda siempre lo mismo.
A continuación se presentan algunos de los términos comunes utilizados en el álgebra.
Coeficiente. Es el número o letra que indica el número de veces que se va a sumar una cantidad.
Ejemplo
Esto se puede representar de la siguiente manera:
e + e + e + e +e + e... = n(e) ---------- ("n" veces la suma de la "e")
Fórmula. Es una regla expresada por medio de símbolos que indica las operaciones que se deben efectuar para obtener ciertos resultados.
Ejemplo
A = b x a, es la fórmula para obtener el área de un rectángulo, multiplicando la base por la altura.
Ecuación. Es una igualdad que sólo es cierta para un valor determinado de uno de sus elementos llamado incógnita.
Ejemplo
6x = 18
Esta ecuación sólo es cierta cuando x = 3, siendo "x" la incógnita.
Miembros de una ecuación. Son las partes de una ecuación que se ubican a cada lado del signo de igual. Así, una ecuación siempre tiene dos miembros, al de la izquierda se le conoce como primer miembro y al de la derecha se le conoce como segundo miembro. Cada uno de los miembros de una ecuación puede tener uno o varios términos.
Ejemplo
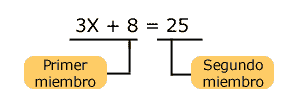
Paréntesis. Es un signo de agrupación que permite indicar qué operaciones se realizan primero, o que al resultado de un conjunto de elementos se le va a aplicar el resultado de otro conjunto de elementos.
Ejemplo
(m + w) - a (m + w)
En esta ecuación, a la suma de "m" y "w" se le debe restar lo que resulte de la suma de "m" y "w" multiplicado por "a"
|
Un producto de literales se puede escribir de cualquiera de la siguientes maneras: a x b, a • b, a b, (a) (b) Sin embargo, cuando se están utilizando literales, se recomienda no utilizar el simbolo de "por" (x), porque se puede confundir con la letra "equis" (x). |
Variable dependiente o función. Es una cantidad que depende de las modificaciones que sufra en una ecuación otra cantidad llamada variable independiente.
Ejemplo
En la ecuación y = ax2 - x + 4, la "y" está en función de "x", porque si se modifica la "x" la "y" también lo hará. En esta ecuación, la "y" es la variable dependiente y la "x" es la variable independiente.
Términos semejantes. Son aquellos que sólo difieren en los coeficientes y tienen las mismas literales.
Ejemplo
2x y 13x son términos semejantes porque sólo varió el coeficiente. También lo son ax y bx porque lo que varía entre ellos es el coeficiente.
Exponente. Es un "numerito" o cantidad que se coloca arriba y a un lado de otro número o literal que se llama base y significa el número de veces que se debe multiplicar por sí misma a la base para obtener un resultado que se llama potencia.
Ejemplo
53 (cinco al cubo), el tres pequeño es el exponente y el cinco es la base. Esto significa que el cinco debe ser multiplicado por sí mismo tres veces, con lo que se obtiene el resultado o potencia (125).
53 = 5 x 5 x 5 = 125
También se puede indicar con literales; por ejemplo, xa en donde "x" es la base y "a" el exponente.
Radicación. Es la operación aritmética que nos permite conocer a la base, cuando se conoce el exponente y la potencia.
Ejemplo
El número que elevado al cuadrado
nos da 49 es 7,
porque |
... |
El número que elevado al cubo
nos da 125 es 5, porque  |
... |
Grado de un término. Es la suma de los exponentes de las incógnitas o literales.
Ejemplo
l2x es de primer grado, ax2 es de segundo grado, xy es de segundo grado (uno de la "x" y otro de la "y"), x2 y3 es de quinto grado (dos de la "x" y tres de la "y").
Grado de una expresión algebraica. Es el mismo que el del término con mayor grado.
Ejemplo
La ecuación
|
|
|
es de tercer grado, debido a que el grado de 12xy2
es tres. |
Monomios, binomios, trinomios y polinomios. Es el nombre que se da a los términos de los miembros de una ecuación de acuerdo al número de partes que están separadas por un signo de más o de menos.
Así, cuando tienen un solo elemento se les dice monomios. Si tienen dos, se llaman binomios; con tres, se les conoce como trinomios y a todas las que tienen más de dos se le llama polinomios. Lo anterior se muestra en los siguientes ejemplos.
Ejemplos
Cantidad
de elementos |
Ejemplo |
Nombre |
| Uno | 2x | Monomio |
| Dos |
2x + 3y |
Binomio |
| Tres |
2x + 3y - 2x2 |
Trinomio |
| Más de dos | 2x + 3y - 2z + 5w | Polinomio |
La expresión 12s - 14r + 3n + 14w tiene cuatro partes y cada una de ellas es un monomio, pero si se le analiza toda junta, se dice que es un polinomio.
En el caso de 3x2 - 4x + 12, como se tienen tres partes será un trinomio.
Presione el siguiente botón y realice la actividad que se propone.
 |
||
 |
 |
 |