Isabel necesita 1
de litro de crema para hacer un postre. Si
en el refrigerador tiene un recipiente con 
de litro de crema y otro con 
litro,
¿le alcanza o tiene que comprar más crema?
Isabel, para conocer si le alcanza la crema que tiene,
debe sumar
y ;
luego, comparar su resultado con lo que necesita (
1
de litro) y con ello definir si le alcanza su crema o tiene que
comprar más.
Suma de lo que tiene:
+
= ?
En esta suma de fracciones, se puede observar que cada una de las fracciones que la componen tienen diferente denominador.
Isabel recordó que para sumar o restar fracciones éstas deben tener el mismo denominador, por lo que decide encontrar fracciones equivalentes con el mismo denominador.
Como tiene las fracciones
y ,
tratará de encontrar una fracción equivalente a
pero con denominador de 4.
= 
Para esto, se debe buscar un número que multiplicado
por 2 de 4. Este número es el 2,
por lo que la fracción equivalente a
con denominador 4 será:
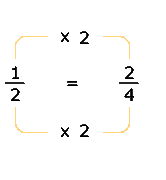
Con esta fracción equivalente, se puede plantear la suma de las fracciones de Isabel, de la siguiente manera:
+ 
=
Con lo que el resultado será la suma de los numeradores con denominador 4.
+
= 
= 
Realizando la conversión a números mixtos se tiene:
 |
= 1  |
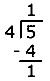Con este resultado, Isabel se da cuenta que
los
de litro y el
de litro de crema que tiene suman 1
litros que es exactamente lo que necesita para hacer un postre,
por lo que no tiene que comprar más crema.
Ejemplo
La señora Araceli tiene un negocio donde vende
quesadillas. Ella fue a visitar por la noche a su comadre para que le
ayudara a calcular cuántos kilos de masa tiene que comprar para
el día siguiente, si por la mañana usó
5
de kg de masa y por la tarde 4
de kg de masa.
En este caso, se trata de una suma de números mixtos.
Entonces, para saber el total de kilos de masa, hay que hacer la siguiente suma:
5
+ 4
=
Primero
Sume los enteros:
5 + 4 = 9
Segundo
Sume las fracciones:
+
=
 |
Recuerde que para sumar fracciones se necesita que todas tengan el mismo denominador. |
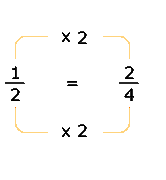Enseguida,
se busca una fracción equivalente a
con denominador 4.
Observe que el 2
se puede igualar al 4 multiplicándolo
por 2.
Ahora tenemos la suma de fracciones con el mismo denominador:
+
=
+
=
=
Araceli se da cuenta que el resultado
es una fracción con el numerador más grande que el denominador,
por lo que conviene convertirlo a número mixto haciendo la división
5 ÷ 4.
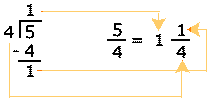
Finalmente, volvemos a sumar enteros con enteros y al resultado se le agrega la parte fraccionaria de la siguiente forma:
9 kg + 1kg
= 10kg
(diez kilos un cuarto)
Otra manera de realizar este tipo de sumas es pasando los números mixtos a decimales y, luego, hacer la suma con la calculadora.
|
Recuerde que para convertir un número mixto a un número decimal sólo se requiere agregar a la parte entera el decimal que resulte de la división de la fracción. |
| Observe:
5
= 5
------ |
÷ |
= 0.75 | ||
3 |
4 |
|||
Entonces: 5
= 5 + 0.75 = 5.75
| También:
4
= 4 +
----- |
÷ |
= 0.50 |
||
1 |
2 |
|||
Entonces: 4
4 + 0.50 = 4.50
Ahora, se suman los números decimales usando la calculadora:
| 5 |
. |
7 |
5 |
+ |
4 |
. |
5 |
= |
10.25 |
Observe que el resultado 10.25 se puede expresar como número mixto haciendo la conversión a fracción de la parte decimal.
| 10.25 kg = 10  kg
= 10kg |
|
Recuerde que 
se simplifica dividiendo entre 25 arriba
y abajo para obtener la fracción equivalente igual a  . |
Ejemplo
Marcos tiene un negocio de cerrajería y sus ingresos mensuales son alrededor de $6,000.00, pero una quinta parte la utiliza para pagar la renta del local y la luz, y una cuarta parte la gasta en materiales.
Marcos desea saber qué parte de sus ingresos usa en su negocio y qué tanto corresponde a sus ganancias.
Marcos piensa que necesita hacer una suma de fracciones.
| La parte de la renta (  ) |
+ | La parte de los materiales
( ) |
= | La parte de los ingresos que se gastan en el negocio |
Para sumar fracciones se necesita que éstas
tengan el mismo denominador. Primero, hay que buscar un común
denominador para las dos fracciones (
y ).
Marcos se preguntó si alguno de
los dos denominadores (el 5 ó el
4) podría servir para ambas fracciones.
|
Recuerde que el común denominador es el número que es divisible entre los dos denominadores (el 5 y el 4) en forma exacta, es decir, sin residuo. |
Primero, probó el 5 y encontró que no funciona porque el 5 no se puede dividir de manera exacta entre 4. Luego, probó el 4 y encontró que tampoco funciona porque el 4 no se puede dividir en forma exacta entre el 5.
Como ni el 4 ni el 5 funcionan como común denominador, Marcos buscó otro número. El número más seguro, aunque no siempre es el más pequeño, resulta de multiplicar los dos denominadores (4 x 5 = 20).
Observe que el 20 sí funciona como común denominador porque sí es divisible entre el 5 y el 4.
20 ÷ 5 = 4 y 20 ÷ 4 = 5
Enseguida, Marcos trató de encontrar las fracciones equivalentes con denominador 20 para cada una de las dos fracciones.
..................
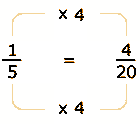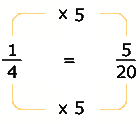
Finalmente, Marcos hizo la suma así:
+
= 
+ 
= 
= 
Observe que
se pueden transformar en porcentaje buscando la fracción equivalente
con denominador 100.
Ingresos
 |
 |
|
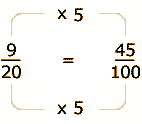| = 0.45 = 45% | ||
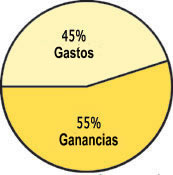
Ahora Marcos sabe que nueve veinteavos
(),
o el 45% de sus ingresos, los gasta en su
negocio y el resto (55%) es la ganancia que
se lleva a su casa.
Ejemplo
El otro día fueron a visitar a don Paco tres amigos que tenían una granja de pollos en sociedad y habían decidido cerrar porque no les había ido bien. Les sobraron 35 pollos que ahora querían repartirse, de acuerdo con la participación que cada uno tenía en el negocio.
A
uno de los socios le pertenecía la mitad del negocio, mientras
que a los otros dos les correspondía 
y 
,
respectivamente.
Como no se ponían de acuerdo de cuántos pollos les tocaban a cada uno, fueron a ver a don Paco para que les ayudara a hacer el reparto.
El problema que tenían era que al dividir la cantidad de pollos entre la parte que les correspondía les resultaban cantidades con decimales y no querían partir los pollos.
| () |
35 | ÷ | 2 | = | 17.5 |
| () |
35 | ÷ | 3 | = | 11.6666 |
| () |
35 | ÷ | 9 | = | 3.8888 |
Don Paco se dio cuenta del fondo del problema y, tomando ventaja de sus conocimientos de fracciones, aceptó ayudarles a resolver el asunto.
Don Paco les aseguró que con la solución que él tenía, todos iban a salir ganando.
Como don Paco tenía pollos, les ofreció prestarles uno para completar 36 pollos y así tener una cantidad más fácil de repartir sin necesidad de partir ninguno.
Así, al que tenía la novena
parte del negocio le tocaban 4 pollos (porque
=
4), en lugar de los 3.888 que le
correspondían.
Al socio que tenía la tercera parte
le tocaron 12 pollos (porque 
= 12), en lugar de los 11.666 que
le correspondían.
Al que tenía la mitad del negocio
le tocaron 18 pollos (porque 
= 18), en lugar de 17.5 que le correspondían.
Como
sobraron dos pollos, don Paco recuperó el pollo que les había
prestado y sus amigos no tuvieron inconveniente en que se quedara con
el otro pollo como pago por sus servicios.
Asombrados por la astucia de don Paco, los tres amigos se despidieron muy agradecidos.
¿De qué se dio cuenta don Paco para tomar ventaja del problema de sus amigos?, ¿a qué se debe que todos salieron ganando?
Don Paco se dio cuenta que había
un error en las participaciones de los socios (,
y
)
porque la suma de las partes no correspondía con la unidad o
el todo.
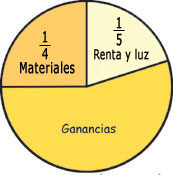
Don Paco representó el negocio de la granja o lo que quedaba
de ésta (los 35 pollos) con un círculo,
así:
Luego, representó en el círculo
las participaciones de los tres socios
(,
y
).
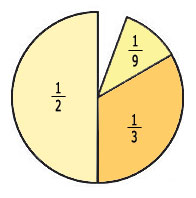
Y observó que quedaba una fracción
sin repartir, de la cual los tres socios no se habían percatado.
En la figura se puede ver que la fracción faltante podría
ser un poquito menor a .
Don Paco pensó que alguno de los tres socios tenía equivocada su participación o fracción del negocio.
|
Recuerde que la suma de todas las fracciones que componen un todo debe ser igual a uno. |
Para saber la cantidad de la fracción
que falta, sólo basta sumar las fracciones (
+
+ )
y determinar por diferencia lo que falta para que sume uno.
+
+
=
|
Recuerde que para sumar o restar fracciones se necesita que todas tengan el mismo denominador. |
Deberá buscar fracciones equivalentes que tengan el mismo denominador, por lo que hace lo siguiente:
Busca el menor número posible que divida de manera exacta al 2, 3 y 9.
Prueba con el número más chico de los tres que es el 2, pero ni el 3, ni el 9 son divisibles entre 2. Lo mismo sucede con el 3 y el 9, por lo que prueba el producto de los tres números: 2 x 3 x 9 = 54, número que sí es divisible entre 2, 3 y 9.
Ahora, deberá encontrar las fracciones equivalentes con denominador 54.
a) .
= 
....b)..
= ....c)
=
Observe que si divide el común denominador (54) entre el denominador de la fracción que se tiene (2, 3 ó 9), se obtiene el número por el que se debe multiplicar el numerador para encontrar la fracción equivalente.
Esto es: ...a) 
x 1 = 27 ...b) 
x 1 = 18 ...c)
x 1 = 6
Esto significa lo mismo que:
a)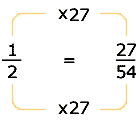
..b)
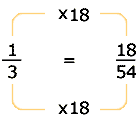..c)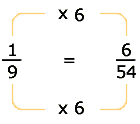
La suma quedará de la siguiente manera:
+ 
+ 
= 
= 
Para encontrar la cantidad que no está reportada en la sociedad,
se deben restar a 1 los .
Recordando que 1 = 
,
se tiene:
Esta fracción (
)
se puede representar por una equivalente de menor denominador ya que tanto
el 3 como el 54
se pueden dividir entre 3.
=  |
|
Recuerde que una fracción no se altera si su numerador y denominador se multiplican o dividen por un mismo número. |
En resumen, para sumar o restar fracciones con diferente denominador, se pueden seguir los siguientes pasos.
1. Busque un denominador común (el menor que sea posible) que pueda ser dividido entre todos los denominadores de las fracciones.
+ 
+ 
= 
En este caso, ninguno de los tres denominadores (6, 9 y 3) divide a los otros dos de manera exacta, por lo que se puede probar con el producto de los tres (6 x 9 x 3 = 162) o con otro número menor que pueda ser dividido por los tres (se puede probar con el 18).
18 ÷ 6 = 3
18 ÷ 9 = 2
18 ÷ 3 = 6
Aun cuando el resultado sería el mismo al usar cualquiera de los dos números (18 ó 162), es más fácil utilizar el menor.
2. Obtenga una fracción equivalente de cada una de las tres que se van a sumar, pero con denominador 18.
......
......
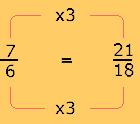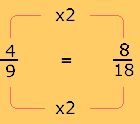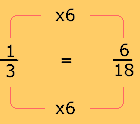
3. Ahora, sume las tres fracciones equivalentes que tienen el mismo denominador.
+
+
= 
+ 
+ 
= 
=
4. Cuando tenga fracciones con numerador mayor que el denominador, convierta a un número mixto.
............
............
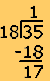= 1 
Ejemplo
+ 
+
=
Paso 1
Busque un común denominador que sea divisible por todos los denominadores
de las fracciones a sumar. El número que es dividido por los denominadores
(7, 5, 3) puede ser el producto de tres denominadores.
7 x 5 x 3 = 105
+
+
= 
Paso 2
Obtenga las fracciones equivalentes de ,
y
con denominador 105.
= ,
=
y
=
.....
......
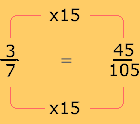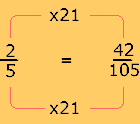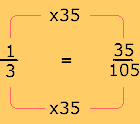
Observe que los números por los que hay que multiplicar a los dos términos de las fracciones (15, 21 y 35) se obtienen al dividir al común denominador (105) entre el denominador de la fracción correspondiente. Por ejemplo, 105 ÷ 7 = 15. Cantidad por la que se debe multiplicar el numerador y denominador para obtener la fracción equivalente.
Paso 3
Se suman las fracciones equivalentes con el mismo denominador.
+
+
= 
+ 
+ 
= 
Paso 4
Se obtiene el número mixto.
...............
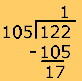= 1 
Presione el siguiente botón y realice la actividad que se propone.
 |
||||
 |
 |
 |
||