| |
|
| Tema 2 - Proporciones | |||||||||||||||||||||||||||||||||||||||||||||
|
Conversión de decimales a fracciones En las unidades anteriores se hizo una presentación de las fracciones y cómo se utilizan en algunos ámbitos. También se insistió en que todas las operaciones (suma, resta, multiplicación y división) con fracciones se pueden realizar con gran facilidad al convertir a las fracciones en decimales. Pero en algunas ocasiones se requiere que los resultados de esas operaciones sean presentados en quebrados, por lo que a continuación se presentan algunas recomendaciones para hacer dicha conversión. Conversión de las fracciones más comunes. En el hogar o en el comercio es común utilizar las siguientes fracciones:
Al realizar las divisiones de estas fracciones se obtiene su equivalencia en decimales:
Lo anterior significa que cada vez que se tenga una fracción en forma de quebrado, ésta puede ser convertida a decimal. Así por ejemplo, tenemos:
Con el simple hecho de recordar las equivalencias en quebrados de los decimales 0.25, 0.333, 0.5, 0.666 y 0.750, se puede hacer la conversión de manera automática. Con las fracciones convertidas a decimales, se pueden hacer todas las operaciones que en la vida cotidiana son necesarias. Observe usted:
Y como se sabe que 0.5 es igual , se puede decir que,
De la misma manera se pueden realizar otras operaciones, como las siguientes, y poner sus resultados en decimales o en quebrados. 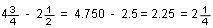 |
||||||||||||||||||||||||||||||||||||||||||||
| Secretaría de Educación Pública Instituto Nacional para la Educación de los Adultos Universidad Autónoma de Yucatán Facultad de Matemáticas Mérida, Yucatán, México, Enero 2003 |