
Ambrosio va a pintar un muro del que conoce la dimensión de su base pero le falta la altura porque no cuenta, por el momento, con una escalera para medirla.
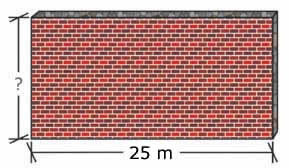 |
¿Cómo podría Ambrosio conocer la altura del muro y con ello poder calcular el área que va a pintar? |
Ambrosio puede más o menos calcular la altura del muro parándose junto a él y marcar su altura con un gis, luego alejarse y calcular cuántas veces cabe su altura en el muro. Pero este procedimiento no es muy preciso, pues está suponiendo cuántas veces cabe su altura en el muro para luego multiplicarla.
Una forma de calcular la altura del muro, con mucha mayor precisión, es utilizando la geometría, por medio de las razones semejantes. Observe usted lo que hace Ambrosio:
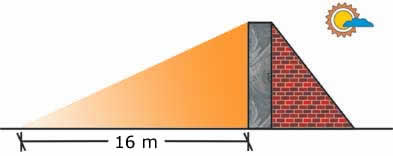
La sombra que da el Sol cuando pasa por el muro a las 11 a.m. mide 16 m.
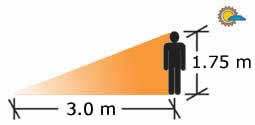 |
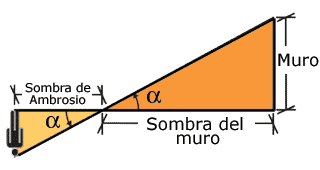
La sombra de Ambrosio, también a las 11 a.m., es de 3.0 m y él sabe que mide 1.75 m. Con esta información él podrá calcular la altura del muro, ya que si usted observa los dos dibujos, en cada uno de ellos hay un triángulo rectángulo semejante. |
Lo anterior se aprecia mejor si se dibuja de la siguiente manera:
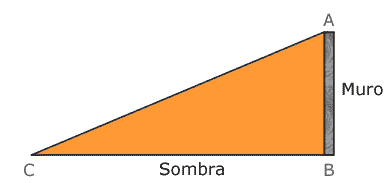

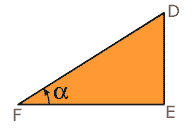
De la misma manera se puede analizar a Ambrosio y su sombra.
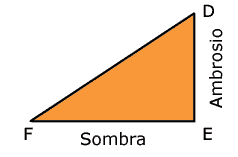

Observe que los triángulos ABC y
DEF son semejantes porque sus tres lados
son proporcionales. Esto quiere decir que la relación que existe
entre el alto del muro y su sombra (![]() )
es la misma que existe entre la altura de Ambrosio y la longitud de su
sombra (
)
es la misma que existe entre la altura de Ambrosio y la longitud de su
sombra (![]() ).
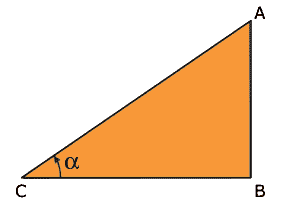
Esto es porque los dos triángulos (ABC
y DEF) tienen el mismo ángulo
).
Esto es porque los dos triángulos (ABC
y DEF) tienen el mismo ángulo![]() (se
lee alfa).
(se
lee alfa).
 |
 |
La sombra del muro |
La sombra de Ambrosio |
| Utilizando el álgebra se puede decir que: |
 |
| Por lo anterior se tiene que: |
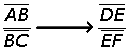 |
También se podría haber dicho que:
La altura del muro AB es proporcional a la altura de Ambrosio DE.
 |
Y que la sombra del muro BC es proporcional a la sombra de Ambrosio EF, desde luego, ambas medidas a las 11 a.m.
 |
Ahora Ambrosio tiene una ecuación en la que conoce tres variables y tiene una incógnita.
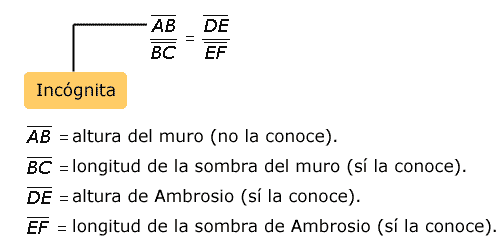
Con lo anterior puede plantear una ecuación como la siguiente:
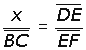 |
(x= altura desconocida del muro) |
| Despeja la incógnita "x", por lo que multiplica a los dos miembros de la ecuación por BC: |
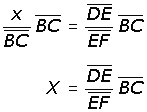 |
| Sustituyendo se tiene: |
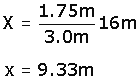 |
Con esto Ambrosio sabe que el muro tiene una altura de 9.33 m, lo que multiplicado por los 25 m que tiene de base obtendrá su área.
| 9.33 m x 25 m = 233.25 m2
|
 |
Recuerde usted que cuando tiene figuras que son semejantes, conociendo la relación que existe en ellas, se puede estimar cualquier dimensión que falte. |
En el caso del muro de Ambrosio, la semejanza se puede comprobar de la siguiente manera.
Forma algebraica:
Cuando se obtiene la misma cantidad en los dos triángulos al dividir a uno de los lados entre otro de sus lados.
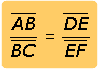 |
Forma gráfica:
1. Cuando un triángulo cabe exactamente en una parte del otro.

2. Cuando, al continuar las líneas de un ángulo formado, se puede colocar el otro triángulo pero de manera simétrica:
Observe que en ambos casos el ángulo![]() es el mismo.
es el mismo.
Martín necesita medir el ancho del río que pasa cerca de su propiedad, pero no puede llegar al otro lado. ¿Cómo podría medir el ancho del río?

Para resolver su problema, Martín hace lo siguiente:
1. Identifica un punto determinado al otro lado del río, en donde quiere medir el ancho del río, por ejemplo el árbol (Punto A).
2. Del punto identificado (el árbol), traza una línea imaginaria sobre la longitud que quiere medir. Ésta debe ser perpendicular al cauce del río para que la medida que obtenga sea la adecuada (Punto B).
3. Se desplaza a uno de los lados del punto de observación, también de manera perpendicular, a una distancia considerable (Punto C).
4. De ahí camina de manera perpendicular al cauce, alejándose del río para establecer un segundo punto de observación (Punto D), a una distancia de 3 m.
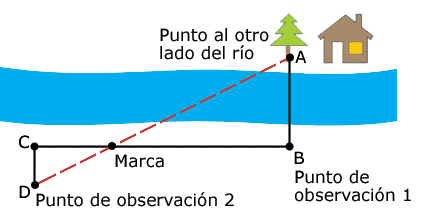
5. Martín, desde el punto de observación 2, ve hacia el punto de referencia al otro lado del río y pide ayuda para que por donde pasa la línea imaginaria que resulta al mirar el punto de referencia desde el punto D, se ponga una marca (Punto E).
Ahora Martín tiene dos triángulos semejantes, como se muestra en el siguiente croquis:
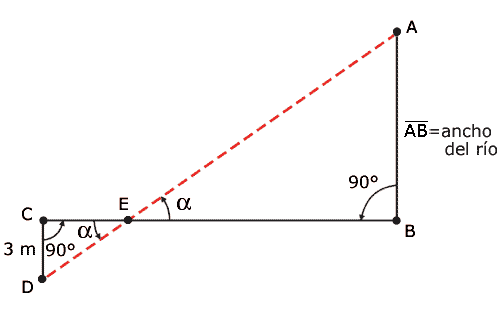
Si observa el croquis, se dará cuenta que los triángulos ABE y ECD son semejantes por lo que se puede plantear que:
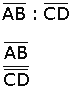 |
| y que: |
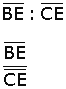 |
| Como los dos triángulos son semejantes, se dice que: |
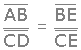 |
Y como lo único que no se conoce de esta ecuación
es ![]() (el
ancho del río), este segmento se despeja de la siguiente manera:
(el
ancho del río), este segmento se despeja de la siguiente manera:
Se multiplican a ambos términos por ![]() :
:
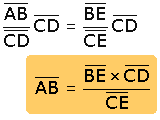 |
Con esta ecuación, Martín podrá calcular el ancho del río.
Observemos qué sucede si se tienen los siguientes datos:
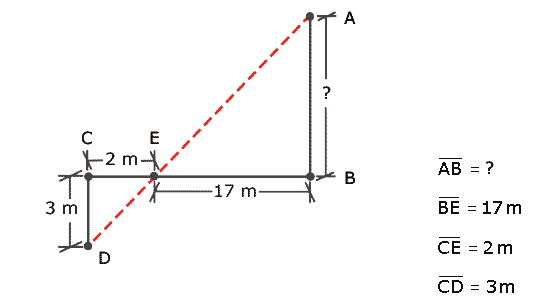
Aplicando la fórmula obtenida se tiene:
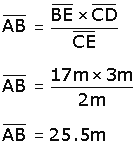 |
Con esto Martín sabe que el río tiene un ancho aproximado de 25.5 m.
Las razones de semejanza no se deben aplicar de manera
directa cuando se manejan relaciones cuadráticas, como las áreas.
Observe lo que le pasa a un colocador de pisos.
Mauricio es colocador de pisos y va a colocar mosaico en una habitación que mide 3 m x 4 m.
 ¿Cuántos
mosaicos debe comprar Mauricio si los mosaicos seleccionados miden 0.25
m x 0.25 m cada uno?
¿Cuántos
mosaicos debe comprar Mauricio si los mosaicos seleccionados miden 0.25
m x 0.25 m cada uno?
¿Cuántos mosaicos deberá comprar si los mosaicos seleccionados no alcanzan y se ve obligado a comprar unos que miden, de cada lado, el doble de los seleccionados?
Mauricio piensa así:
El área de la habitación en la que se van a colocar los mosaicos es:
| 3 m x 4 m = 12 m2
|
El área de cada mosaico de 0.25 m x 0.25 m es:
| 0.25 m x 0.25 m = 0.0625 m2
|
Para conocer el número de mosaicos de 0.25 m x 0.25 m, habrá que analizar cuántas veces cabe el área de un mosaico en el área de la habitación.
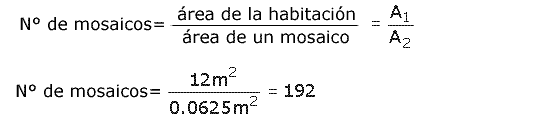
Con lo anterior, Mauricio sabe que necesitará 192 mosaicos de 0.25 m x 0.25 m.
Ahora, para calcular el número de mosaicos que miden el doble que los anteriores Mauricio piensa:
"Si con mosaicos de 0.25 m x 0.25 m ocupé 192 mosaicos, con mosaicos que miden el doble, pues ocuparé la mitad."
Qué opina usted de lo que piensa Mauricio, ¿está en lo correcto?
Veamos aritméticamente si lo que piensa Mauricio es correcto.
La mitad de 192 es:![]() .
.
Y si cada uno de estos mosaicos mide 0.5 m x 0.5 m, observemos qué área se cubre con estos 96 mosaicos de 0.5 m x 0.5 m.
 Área
de los mosaicos de
Área
de los mosaicos de
0.5 m x 0.5 m:
0.5 m x 0.5 m = 0.25 m2
Multiplicando el área de cada mosaico por 96, se tendrá el área que cubren estos mosaicos:
0.25 m2 x 96 = 24 m2
Con lo anterior se observa que si Mauricio compra 96 mosaicos de 0.5 m x 0.5 m cubrirá 24 m2 y él sólo requiere cubrir 12 m2. Esto indica que está equivocado y que compraría mosaicos de más.
Entonces, no debe aplicar una razón de semajanza lineal, sino dividir el área a cubrir entre el área de cada mosaico.
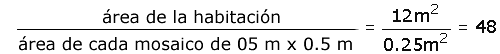
Esto nos indica que Mauricio necesitaría 48
mosaicos de 0.5 m x 0.5
m para cubrir 12 m2.
