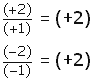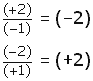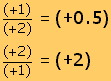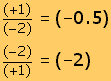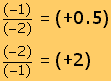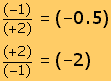Para poder realizar cualquier operación
de números con signos, es necesario conocer las leyes de los signos,
que se presentan a continuación.
Al multiplicar un número por 1
(la unidad), se obtiene el mismo número; por lo que se puede escribir
lo siguiente:
(-2) (1) = - 2
Observe que para multiplicar no se usa el signo "x",
con ello se evita confundirse con una "equis". Así, para
indicar un producto, se usará un punto o un paréntesis entre
las cantidades .
Observe que un número con signo negativo multiplicado por un número
con signo positivo da como resultado un número con signo negativo
(-).
(-)(+) = (-)

En la recta numérica, se observa que multiplicar a -2 por 1 se obtiene -2.
Al multiplicar números con signo diferente se obtienen números con signo negativo.
| (-) | (+) = | (-) |
| (+) | (-) = | (-) |
Así, (2) (-4) = -8, porque se está multiplicando dos veces al -4.

Lo mismo sucederá si se pone primero el negativo y luego el positivo.
(-4) (+2) = (-8)
Al multiplicar un número negativo por otro número negativo, se tendrá como resultado un número positivo: (-) (-) = (+).
(-1) (-2) = 2
Esto se explica al recordar que todo número multiplicado por la unidad da el mismo número. Si la unidad fuera negativa, habría que cambiar el signo del número que se multiplica.
(-1) (-2) = 2
También, si se multiplica a un número positivo por otro positivo, se tendrá otro positivo.
(+1) (+2) = (+2)
Al multiplicar números con el mismo signo
se obtendrán productos con signo positivo.
| (-) | (-) = | (+) |
| (+) | (+) = | (+) |
Las leyes de los signos para operaciones se sintetizan en la siguiente tabla.
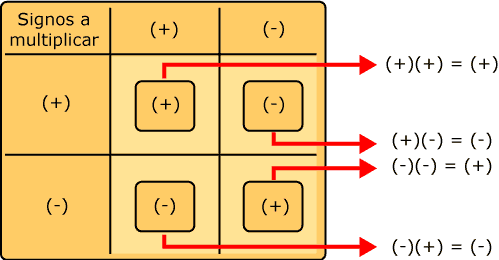
A continuación, se puede observar cómo se aplican las leyes de los signos para la multiplicación.
| Producto
de signos contrarios da un signo negativo. |
Producto de signos iguales da un signo positivo. |
| Ejemplos | Ejemplos |
| (+3)
(-2) = (-6) (-3) (+2) = (-6) (+4) (-1) = (-4) (-12) (+2) = (-24) (-6) (+3) = (-18) (-12) (0) = (0) |
(+3)
(+2) = (+6) (-3) (-2) = (+6) (+4) (+1) = (+4) (-12) (-2) = (+24) (-6) (-3) = (+18) (-12) (0) = (0) |

| Observe que al multiplicar pueden ser cambiados de lugar el multiplicador y el multiplicando y el producto no se altera. |

| Recuerde que las leyes de
los signos son: (-) (-) = (+), (+) (+) = (+), (-) (+) = (-) y (-) (+) = (-). |
Las reglas que se obtuvieron para la multiplicación funcionan perfectamente en el caso de la división de los números con signo, como se observa a continuación.
| La división
de signos iguales da un signo positivo. |
La división de signos diferentes da un signo negativo. | ||||
| |
|
||||
| Ejemplos
|
Ejemplos
|
Observe que en la división, al cambiar de lugar al divisor y al dividendo, se modifica el resultado de la división, pero no los signos.
Ejemplos
|
|
||
|
|

| Recuerde que la división de signos iguales da un signo positivo, y la división de signos diferentes da un signo negativo. |
Ejemplos
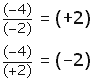
|
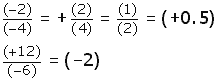 |
Presione el siguiente botón y realice la actividad que se propone.
Las leyes de los signos se aplican en todas las operaciones de los números con signo.
Observe usted cómo se presentan los números con sus signos y en medio el signo de la operación.
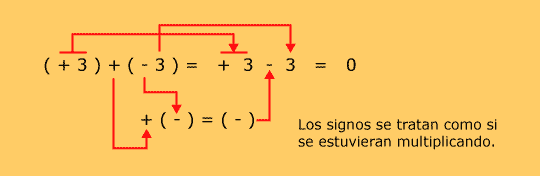
(+3) + (-3) = ?
Para resolver esta operación, es necesario eliminar los paréntesis de los números con signo. Se deben aplicar las reglas de los signos, como se muestra a continuación:
 |
 |
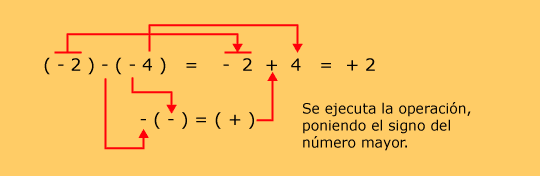 |
Observe que como el (-2)
no tiene signo antes del paréntesis, se pone el mismo signo negativo,
ya que equivale a tener un signo positivo antes, y
(+) (-) = (-)
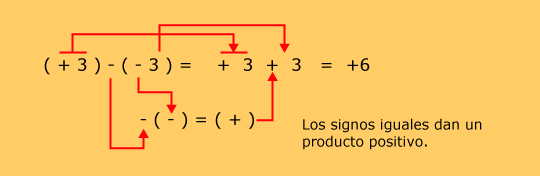
Para que el procedimiento sea más claro, se pueden definir los pasos necesarios para resolver una operación con signos.
(-4) - (-8) = ?
Esta operación se lee "menos cuatro, menos, menos ocho".
Primero
Elimine los paréntesis aplicando las reglas de los signos.
Como el (-4)
no tiene un signo antes del paréntesis se considera como (+);
por lo tanto, de acuerdo con las leyes de los signos tenemos que +
(-4) = -4.

| Recuerde que signos iguales dan (+) y signos contrarios dan (-). |
Segundo
Ejecute la operación sin paréntesis; en este caso, restar,
poniendo el signo del número mayor.
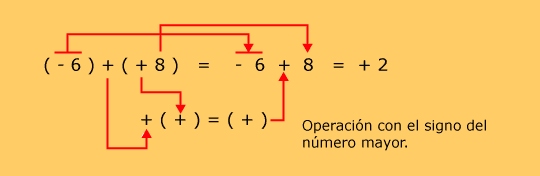
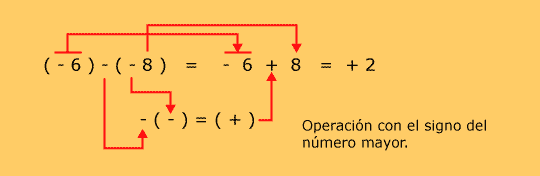
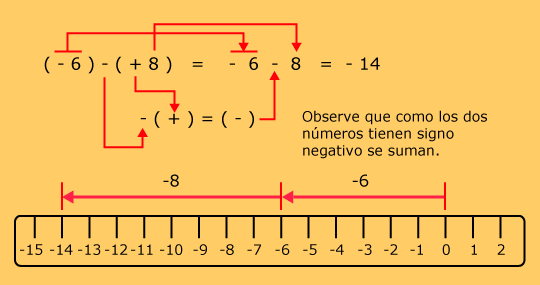
(-4) - (-8) = - 4 + 8 = + 4
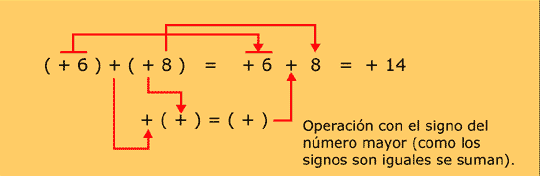
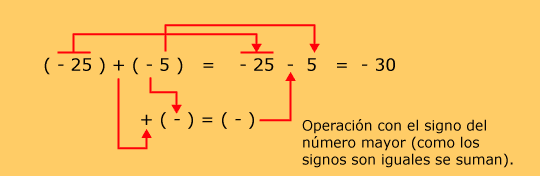
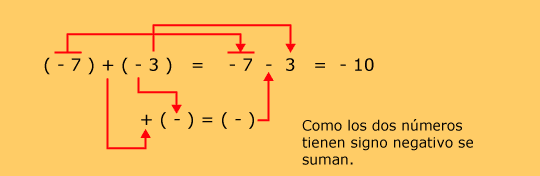
Ejemplos
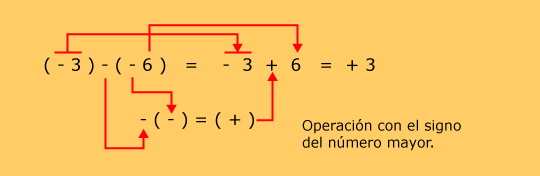 |
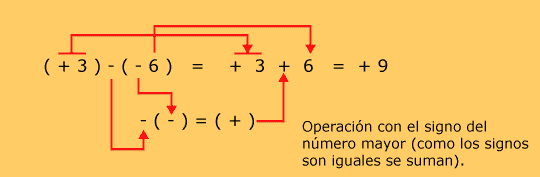 |
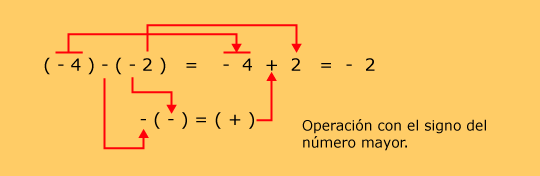 |
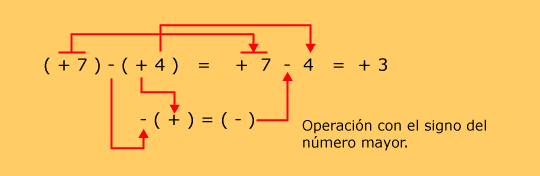 |
 |
 |
 |
 |
 |
 |
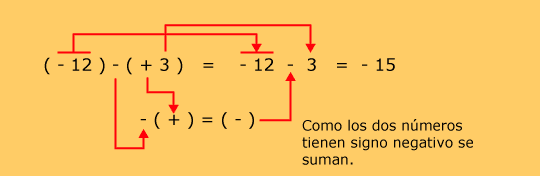 |

| Observe que cuando se multiplica, no se pone nada entre los paréntesis. |
Presione el siguiente botón y realice la actividad que se propone.
Las operaciones con signos pueden estar combinadas, como se muestra a
continuación:
(-2) + (-3) - (-2) - (-1) - (-3) = ?
Para resolver esta operación, primero, se deben quitar todos los paréntesis:
-2 -3 + 2 + 1 + 3 = ?
Se suman todos los números con el mismo signo, y conservan su signo original.
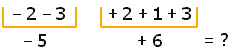
Se resuelve la operación:
- 5 + 6 = + 1
Ejemplos
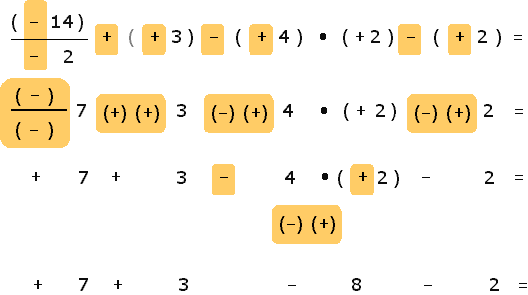
Se suman los positivos y los negativos, poniendo su signo.
+ 10 - 10 = 0
Se ejecuta la operación con el signo del mayor. Como el "0" no tiene signo no se pone ningún signo.
En este otro ejemplo se pueden tratar los signos de la siguiente manera:
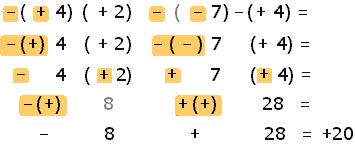
Observe que las operaciones de los signos en este ejemplo se realizaron en un solo paso, de la siguiente manera:


| El punto, al igual que los paréntesis indica multiplicación. |