Al finalizar la semana, Juan y Alicia reciben su pago por la cantidad de miel que venden. Ahora quieren saber quién de los dos cobrará más.

Alicia vendió 7 frascos de litro y Juan vendió 15 frascos de de litro.

Para saber cuál de los dos vendió más, se necesita comparar , que representan las ventas de Alicia, con , que representan las ventas de Juan, y determinar cuál de las dos fracciones es mayor o si son iguales.

Para comparar dos fracciones, se necesita que ambas estén refiriéndose a las mismas partes que representan, por lo que las dos deberán tener el mismo denominador.

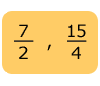
Se escoge para convertirla a cuartos: =


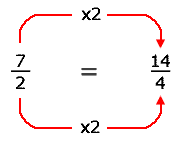
Se multiplica arriba y abajo por 2 para encontrar la fracción equivalente con denominador 4.

Comparando y nos damos cuenta que es menor que .

Por lo tanto, Juan vendió un poco más que Alicia.

Ejemplo

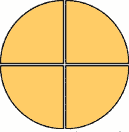
Mateo vende quesos frescos de cabra; para venderlos más rápido los divide en varias partes; un queso lo parte en cuatro partes iguales, así:

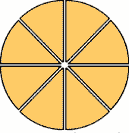
Otro queso lo parte en ocho partes iguales, así:

Algunos clientes prefieren comprar porciones de y otros las prefieren más chicas: de .

Por la tarde, Mateo se da cuenta que en la mañana vendió tres porciones del queso que dividió en 4 partes iguales ( ) y 5 porciones del queso que partió en 8 partes iguales ( ). Ahora Mateo quiere saber de cuál queso vendió más.

Casi sin pensar, Mateo cree que el queso que partió en 8 partes se vende más rápidamente porque de éste lleva 5 porciones vendidas mientras que del otro sólo vendió 3.

Para ver si Mateo tiene razón, hagamos la comparación de la fracción que representa las porciones vendidas del queso dividido en 4 partes con la fracción que representa las porciones vendidas del otro queso.

Porciones vendidas del queso dividido en 4 partes: 3 4

Porciones vendidas del queso dividido en 8 partes: 5 8

La fracción que tenga el mayor valor nos indicará el queso que se vende más rápidamente.

Observe que y tienen diferente denominador y, para comparar dos fracciones, se necesita que ambas tengan el mismo denominador.

Para solucionar lo anterior, sólo basta encontrar las fracciones equivalentes de y de modo que ambas tengan el mismo denominador.

Vea primero si la fracción con el menor denominador puede cambiarse a una fracción equivalente con el mismo denominador de la otra fracción. Como éste es el caso, porque el 8 es divisible entre 4, entonces sólo se necesita buscar la fracción equivalente de con denominador 8.


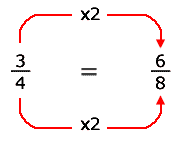
Multiplicando el numerador y el denominador por 2 se obtiene la fracción equivalente de con denominador 8: .

Comparando las fracciones con el mismo denominador nos damos cuenta que 6 es mayor que 5.

Entonces, > , por lo tanto, > .

Por lo tanto, contrario a lo que piensa Mateo, el queso dividido en cuatro partes iguales se está vendiendo más rápidamente que el que partió en ocho partes.

Algunas veces es más fácil convertir las fracciones en decimales y luego comparar.

Ejemplo

= 0.750

= 0.625

Como 0.750 > 0.625, entonces, > .

Para comparar dos fracciones y saber cuál es mayor, conviene transformar las fracciones a sus equivalentes de modo que ambas tengan el mismo denominador.

Ejemplo

Se quiere saber qué fracción es mayor: ó .

Paso 1
Transforme las fracciones a sus equivalentes de modo que ambas tengan el mismo denominador.

Vea primero si alguno de los denominadores funciona como común denominador. Como el 3 no es divisible entre 7 ni el 7 es divisible entre 3, entonces buscamos otro número. El producto 3 x 7 = 21 nunca falla.
Entonces, las fracciones equivalentes con denominador 21 son:

Paso 2
Compare los números de las nuevas fracciones con denominador común.

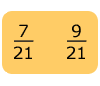
La fracción con el numerador mayor es la fracción de mayor valor.

Como 7 < 9, entonces, <

por lo tanto, < .

Para comprobar los resultados, conviene hacer las divisiones con la calculadora, convirtiendo las fracciones a decimales y luego haciendo las comparaciones en números decimales.

Ejemplo

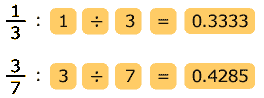
Como 0.3333 es menor que 0.4285, entonces, < .