Experimento 13
¿Cómo determinar el volumen de las rocas?
 
   
     
 

Nuestro planeta, tal y como se conoce, es el resultado de transformaciones y cambios a lo largo de muchos años. Hace mucho tiempo no había agua, ni oxígeno ni vida en la Tierra. Los cambios en la Tierra toman en ocasiones segundos o minutos, como en el caso de la erupción de los volcanes, que expelen gases, rocas y lava; o miles de años, como es el movimiento de los continentes. La superficie de la Tierra está hecha de piedras y rocas que se encuentran en todos lados: cubiertas de agua en el fondo de los océanos, mares, ríos y lagos; fragmentadas en pedazos muy pequeños, como la arena; o formando parte de las montañas.
 
 
 
 

Aprender a medir el volumen de objetos irregulares, como las rocas.
     
 
     
 
  • Una lata. Dependiendo de su tamaño será el tamaño de las rocas, cuyo volumen pueda medirse. Las latas de refresco pueden usarse para rocas pequeñas.
  • Una botella o vaso.
  • Un pedazo de hilo.
  • Diferentes piedras, de la mayor variedad posible: piedra pómez, granito, piedra volcánica, etc.
  • Una regla o flexómetro.
  • Una cinta adhesiva o masking tape.
  • Un bolígrafo.
  • Libros.
     
 
     
 
1.
Con la regla y el bolígrafo marque una escala en centímetros sobre el masking tape y péguelo al costado de la botella, a fin de graduarla.
  
       
 
2.
Para graduar el vaso, agregue en él un volumen conocido de agua, por ejemplo la que cabe en una botella pequeña de cerveza o refresco. Identifique la altura hasta la que llegó el agua en la cinta y con eso podrá indicar en la cinta un volumen que corresponda a la mitad y luego otra vez a la mitad. Si su bote tiene mayor capacidad agregue otra botella de líquido y marque de la misma manera que lo hizo antes.
  
       
 
3.
Corte la lata como se indica en la figura 3 y doble el pedazo cortado.
  
       
 
4.
Llene la lata con agua hasta el límite.
  
       
 
5.
Coloque el vaso graduado de forma que pueda recibir el agua que se desborde del bote.
  
       
 
6.
Amarre cada piedra con el hilo y sumérjala en el agua. Mida cuánta agua se desplaza en el vaso graduado. Si una de las piedras flota (la piedra pómez, por ejemplo), empújela hacia abajo con un alfiler, hasta que esté completamente cubierta por el agua.
  
       
 
7.
El volumen de agua desplazado es igual al volumen de la piedra.
  
       
 
8.
Si le es posible pese cada una de las piedras con una balanza, en la Tierra el peso de un objeto equivale a su masa.
  
     
 
     
  Llene el siguiente cuadro.
     
 
Piedra Características externas Volumen Masa Densidad
1 pómez blanca, llena de agujeros
2
3
4
  * La densidad se calcula empleando la formula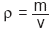
     
 
1.
Explique por qué el agua se desborda.
     
   
     
 
2.
¿Qué resultado obtiene si no sumerge completamente la piedra pómez?
     
   
     
 
3.
La forma de las piedras, ¿afecta su volumen? ¿Cómo lo comprobaría?
     
   
     
 
     
 
1.
Explique lo que concluye de la realización de este experimento.
     
   
     
 
2.
Compare sus resultados con los de sus compañeros del círculo de estudio.
     
   
     
 
     
  Una canción antigua
     
 

“De piedra ha de ser la cama
de piedra la cabecera,
la mujer que a mí me quiera
me ha de querer de a de veras”

¿Por qué las camas de piedra son tan duras?

¿En qué se relaciona lo que aprendió sobre la presión en la Unidad 2 del Libro del adulto y esta cama de piedra?

Si la cama fuera de piedra pómez, ¿sería igual de dura?

Estime cuál sería el volumen de una cama como la suya.

¿Sería diferente el volumen si la cama fuera de piedra?
     
 
     
 
¿Se cumplió con el propósito de este experimento? ¿Por qué?
     
   
     
 
Explique si los resultados que obtuvo de este experimento son útiles en su vida cotidiana.
     
   
     
  De esta actividad podemos concluir que:
     
  a)
El volumen de los objetos irregulares puede determinarse midiendo la cantidad de agua que desplazan, al hundirse en ella.
     
  b)
El volumen de las piedras no depende de su masa.