Varios de los aparatos electrodomésticos que hay en casa funcionan accionados por motores eléctricos (por ejemplo, refrigerador, licuadora, máquina de coser, etc.) En la Fig. 1 (a) mostramos un tipo muy común de motor eléctrico que transforma la energía eléctrica (energía de cargas eléctricas) en energía mecánica o movimiento.
Consideremos un motor eléctrico M, conectado a una batería que le aplica un voltaje VAB, haciendo pasar a través de él una corriente i, Fig. 1 (b). Una característica importante de un motor es su potencia P, la cual se mide en watts (joule/s) y representa la cantidad de energía mecánica (trabajo) que el motor desarrolla en cada segundo.
Para calcular esa potencia, supongamos que el motor mostrado estuviera funcionando durante un tiempo t y que durante ese tiempo, una carga q haya pasado a través del motor de A hacia B (transportada por la corriente i). Siendo T el trabajo realizado sobre esa carga (energía transferida) sabemos que:

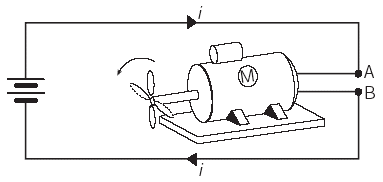
Fig. 1 (a) y (b) Los motores eléctricos son dispositivos que transforman la energía eléctrica en energía mecánica.
![]()
T = q VAB
Un aparato eléctrico sometido a una diferencia de potencial VAB, alimentado por una corriente i, desarrolla una potencia P dada por:
P = i VAB
Es un hecho conocido que, cuando una corriente eléctrica pasa por una resistencia, ésta se calienta. Este fenómeno denominado Efecto Joule, puede observarse en la Fig. 2 (a), que muestra un filamento metálico (una resistencia) calentado, hasta enrojecerse por el paso de la corriente eléctrica. Podemos entender por qué ocurre ese calentamiento, al recordar que los electrones en movimiento, y que constituyen la corriente eléctrica, están chocando constantemente contra los átomos de la red cristalina del filamento. Esos choques aumentan la energía de vibración de esos átomos y sabemos que eso implica un aumento de temperatura de la sustancia.
Supongamos que, entre los puntos A y B de la Fig. 1 (b), hubiéramos sustituido el motor por una resistencia R, como lo muestra la Fig. 2 (b); por tanto, estamos tratando con una situación muy semejante al caso del motor, pero ahora, la energía eléctrica se transforma integralmente en energía térmica. Es evidente que la expresión P = i VAB podrá usarse también en el caso del cálculo de la potencia térmica desarrollada en R. Sin embargo, podemos expresarla también de otra manera pues, en el caso de una resistencia R, tenemos:
VAB = Ri
La potencia térmica desarrollada debida al Efecto Joule es una resistencia R, alimentada por una corriente i, sometida a un voltaje VAB, y dada por las expresiones:
P = i VAB o bien, P = Ri2

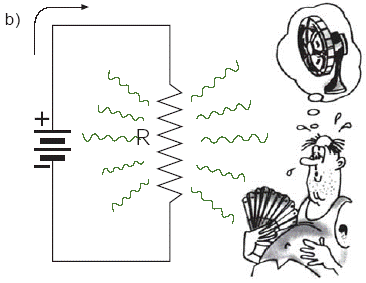
Fig. 2 (a) y (b) Cuando la corriente eléctrica pasa por una resistencia, se calienta. Este fenómeno se denomina efecto Joule.
En el primer ejemplo que resolvimos en
esta sección, al determinar la potencia
P = 720 W desarrollada por el motor, suponíamos
que era nula la resistencia eléctrica de los alambres existentes
en su interior y a través de los cuales la corriente debe pasar
para que el motor empiece a girar (se dice que la resistencia interna
del motor es nula).
Sin embargo, en un motor real, la resistencia interna nunca es nula y así, cuando la corriente eléctrica pasa por el interior del motor siempre hay cierta pérdida de energía debido al Efecto Joule. Por ese motivo un motor eléctrico en funcionamiento siempre está un poco caliente.
Supón ahora que la resistencia interna del motor
analizado fuera R = 2 ![]() .
Como la corriente a través de él era i = 6
A, la potencia térmica PJ disipada por
Efecto Joule en su interior, sería:
.
Como la corriente a través de él era i = 6
A, la potencia térmica PJ disipada por
Efecto Joule en su interior, sería:
PJ = R i 2 = 2
![]() ×
62 A2
×
62 A2
por tanto: PJ = 72 W.
Así, la potencia útil Pu del motor, es decir, la que realmente fue usada para mover la bomba de agua, fue:
Pu = 720 W – 72 W
o bien, Pu = 648 W
La relación entre la potencia útil Pu y la potencia eléctrica P proporcionada por el motor, se denomina eficiencia del aparato. Luego, para el caso analizado, representando la eficiencia por e, tenemos:
![]()
por tanto: e = 0.9
o en forma porcentual: e = (0.9 x 100)%, o bien, e = 90%
Ese resultado significa que el motor convierte en energía mecánica 90% de la energía eléctrica que se le proporciona (10%, es decir, 72 W, se desperdician en forma de calor).
El concepto de eficiencia, tal como se definió (e = Pu / P puede hacerse extensivo a cualquier aparato eléctrico.

Fig. 3 El filamento de este foco se calienta mucho y emite luz.

Fig. 4 Las lámparas fluorescentes emiten luz prácticamente sin calentarse.
Estos dispositivos se usan para impedir que la corriente eléctrica en un circuito o en un aparato sobrepase cierto valor que podría causar calentamiento excesivo y, así, causar daños.
Los fusibles se usan en automóviles, en aparatos eléctricos, en los circuitos de algunas casas. Están formados por un filamento metálico (Fg. 5) que se calienta y se funde cuando la corriente sobrepasa un cierto valor (propio de cada fusible), interrumpiendo el paso de la corriente.
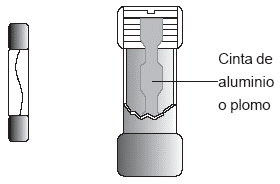
Fig. 5 El filamento de un fusible está proyectado para fundirse cuando la corriente a través de él sobrepasa cierto valor (especificado en el dispositivo por el fabricante).
En funcionamiento normal, un foco conectado a un tomacorriente, Fig. 6, recibe una corriente eléctrica que pasa por el circuito ABCDEF.
Sin embargo, si por algún motivo (por ejemplo, desgaste del recubrimiento de los alambres) hubiera un contacto eléctrico de dos puntos del circuito, como en los puntos B y E de la Fig. 6, una nueva corriente eléctrica será establecida, circulando sólo por el circuito ABEF (ninguna corriente pasará por el foco). Como ese circuito está formado por alambres de conexión, su resistencia es prácticamente nula y, entonces, la intensidad de la corriente en él se hace muy elevada. En virtud del Efecto Joule, hay un incremento considerable de temperatura en esos alambres, que puede provocar efectos desastrosos si no hubiera una protección adecuada (fusibles o interruptor automático).
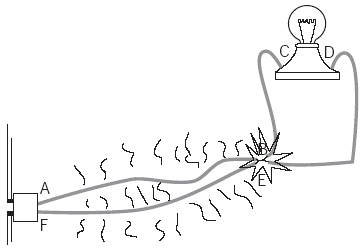
Fig. 6 El corto circuito sucede debido al contacto entre los puntos B y E.
La cantidad de energía eléctrica que se suministra a una casa, se contabiliza con un medidor, semejante al mostrado en la Fig. 7, instalado por la Compañía de Luz. El objetivo de ese aparato es medir la cantidad de energía eléctrica usada en la casa durante cierto tiempo (normalmente 30 días).
Sabemos que:
![]()
por tanto: energía = potencia × tiempo
es decir, E = P × t
Por tanto, cuanto mayor sea la potencia de un aparato electrodoméstico, y cuanto mayor sea el tiempo que este permanece conectado, mayor será la cantidad de energía eléctrica que utilizará. El valor registrado en el medidor equivale a la suma de las energías utilizadas durante cierto periodo por los diversos aparatos instalados en la casa. Esa energía podría medirse en joules (unidades del Sistema Internacional). Sin embargo, en prácticamente todos los países del mundo, las compañías de luz usan medidores calibrados en kwh. Un kwh es una unidad de energía equivalente a 3 600 000 J.

Fig. 7 Medidor de “consumo” de energía eléctrica de una casa habitación.
Considera el siguiente planteamiento presentado en la figura II.17.8; una batería, conectada en serie con un foco y con un recipiente que contiene una solución de sal de cocina (cloruro de sodio, NaCl) en agua. La conexión de la batería con la solución se hace por medio de dos placas metálicas, E1 y E2, denominadas electrodos:
-
E1, conectado al polo positivo de la batería, es el electrodo positivo (o ánodo).
-
E2, conectado al polo negativo, es el electrodo negativo (o cátodo).
Cerrándose el interruptor C, se observa que el foco se enciende, indicando que hay una corriente eléctrica en el circuito. Por tanto, la solución de NaCl (cloruro de sodio) está dejando pasar la corriente a través de esta solución, que es una buena conductora de electricidad. Sin embargo, la conducción de cargas eléctricas en los líquidos (como ocurre en esa solución) se hace de diferente manera que en los metales, lo que analizaremos a continuación.
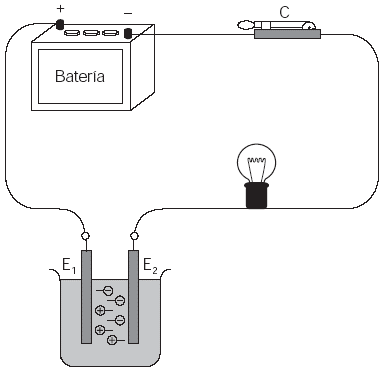
Fig. 8 La corriente eléctrica en los líquidos está formada por iones positivos y iones negativos que se mueven en sentido contrario.
Cuando el cloruro de sodio se disuelve en el agua, los iones de Na+ y Cl– que forman los cristales de esa sustancia se liberan en el interior del líquido. Entonces, en la Fig. 8, el ánodo E1 atrae los iones negativos Cl– y el cátodo E2 atrae los iones positivos Na+. Como esos iones están libres, se desplazan en sentidos contrarios, de la manera en que se muestra en la figura. Ese desplazamiento de cargas positivas para un lado y de cargas negativas para el otro, constituye una corriente eléctrica, equivalente a la que está pasando en las partes metálicas del circuito. Los términos usados en este estudio son:
-
La solución conductora se denomina electrólito.
-
Los iones positivos se denominan cationes (porque se dirigen hacia el electrodo negativo o cátodo).
-
Los iones negativos se denominan aniones (porque se dirigen hacia el electrodo positivo o ánodo).
De modo general, la conducción de la electricidad en un líquido se hace de manera semejante al caso del cloruro de sodio, que acabamos de analizar:
Es evidente que hablar de electrólitos y de iones en solución acuosa, existen serios problemas para poder contar o medir dichas partículas que, como sabemos, son extremadamente pequeñas. Además, para poder manejar de manera práctica los conceptos establecidos en el nivel atómico y molecular, es necesario que se establezcan relaciones que permitan enlazar el mundo microscópico con lo que manejamos en el nivel macroscópico.
En 1811, el científico italiano Amadeo Avogadro estableció una hipótesis en la que afirmaba que “volúmenes iguales de gases diferentes a la misma temperatura y presión contienen igual número de moléculas”. Esta afirmación, que puede parecer aventurada, fue utilizada por los hombres de ciencia para que en condiciones predeterminadas se pudiera saber cuántas moléculas contenía un gas.
Las condiciones que se utilizaron fueron: presión: 1 atmósfera; temperatura: 0 °C y la masa del gas: correspondiente a su masa molecular, expresada en gramos. En las anteriores condiciones, fue posible determinar el número de moléculas, una cantidad que resultó muy grande, pero que se demostró era la misma para distintos gases. Este número se denominó número de Avogrado, en honor del creador de esta teoría, su valor es:
No = 6.023 × 10 23
Este número se convirtió en una unidad de conteo de partículas denominada MOL, es decir:
1 mol = 6.023 × 10 23
Y así como existen unidades de conteo, por ejemplo, la docena (12 piezas), gruesa (144 piezas), podemos también utilizar la mol para referimos a cantidad de piezas o de partículas; así 1 mol de hojas de papel = 6.023 × 10 23 hojas de papel, 1 mol de manzanas = 6.026 × 10 23 manzanas, 1 mol de electrones = 6.023 × 10 23 electrones, 1 mol de iones = 6.023 × 10 23 iones.
Es evidente que la mol, como unidad de conteo, resulta muy grande en nuestra vida cotidiana, por lo que se emplea frecuentemente para contar partículas microscópicas (átomos y moléculas) y aun para contar otras partículas todavía más pequeñas, como son los electrones. Una aplicación directa de las moles se lleva a cabo en la industria de la galvanoplastia (recubrimientos con capas metálicas), en los procesos de plateado, cobrizado, dorado, etcétera.
¿Qué se entiende por potencia de un aparato eléctrico?