Unidad 2. Lectura 2.16
 
Resistencia eléctrica.
 
¿Qué es la resistencia eléctrica?
 

Cuando una corriente eléctrica se establece en un conductor metálico, sabemos que un número muy elevado de electrones libres pasan en movimiento por ese conductor. En este movimiento, los electrones chocan entre sí y también contra los átomos que constituyen la red cristalina del metal (Fig. 1). Por tanto, los electrones encuentran cierta dificultad para desplazarse, es decir, existe una resistencia al paso de la corriente en el conductor.
 
 

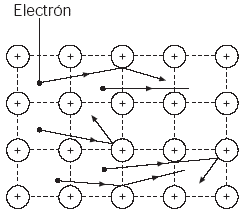
Fig.1 Los electrones libres que forman la corriente eléctrica en un metal chocan contra los átomos de la red cristalina del metal.
 

Para medir esa resistencia, los científicos definieron, como lo mostraremos en seguida, una magnitud que denominaron resistencia eléctrica.

Considera la Fig. 2 que muestra un conductor AB al que recorre una corriente i cuando se le aplica una diferencia de potencial VAB.

Tenemos:
 

Resistencia eléctrica = voltaje aplicado al conductor entre la corriente en el conductor.

Donde: o bien: VAB = Ri

 
Comentarios
 
  1. Supongamos que en la Fig. 2, el voltímetro indicara VAB = 3 V y la lectura del amperímetro fuera i = 0.5 A. La resistencia del conductor AB sería entonces, de acuerdo con la definición:
 
 

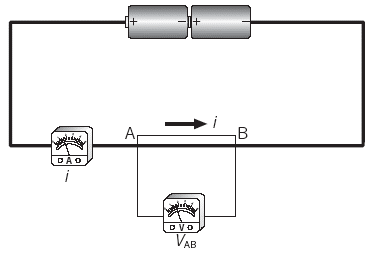
Fig. 2 La resistencia del conductor AB se da por R = VAB / i.
 
 
Vemos que la unidad de resistencia en el Sistema Internacional es volts/amperes, que se denomina ohm en homenaje al científico alemán George Ohm. El símbolo de esa unidad es la letra griega . Entonces:
 
 
Por tanto, la resistencia que calculamos es R = 6 ohms = 6
 
  1. Ahora podemos imaginar que el conductor de la Fig. 2 fuera sustituido por otro, también unido entre los puntos A y B y, por tanto, quedando sometido al mismo voltaje
    VAB = 3 V. Si ese conductor fuera recorrido por una corriente i = 0.3 A (menor que la anterior), podríamos deducir que está ofreciendo mayor dificultad al paso de la corriente, es decir, su resistencia es mayor que la anterior.

De hecho, tenemos:
 
 
 

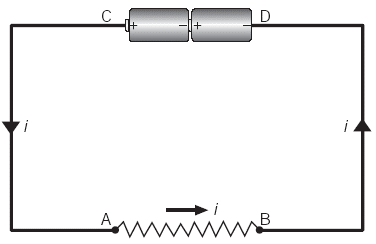
Fig. 3, AB representa un conductor de resistencia R y AC y BD representan conductores de resistencia nula.
 

donde: R’ = 10

o bien, R’ > R

En resumen:
 
Cuando aplicamos el mismo voltaje a varios conductores, aquel que posee mayor resistencia eléctrica será recorrido por la menor corriente.
 
  1. Un conductor que posee resistencia está representado por una línea "quebrada", como lo muestra la Fig.3 (entre A y B).
 
Los alambres que se usan para completar la conexión en el circuito, normalmente tienen resistencia prácticamente nula (R = 0) y se representan por líneas (“no quebradas”), como AC y BD en la figura II.16.3.
 
Ley de Ohm
 

En el circuito que se muestra en la Fig. 4 (a), una resistencia metálica R, sometida a una tensión de 1.5 V, es recorrida por una corriente de 0.1 A (indicada en el amperímetro). En la Fig.4 (b), el voltaje aplicado a R fue duplicado, pasando a 3 V.

Observa que la lectura del amperímetro también se duplicó, pasando a 0.2 A. Si calculamos el valor de R, en el primer experimento, tenemos:
 
 

donde: R = 15 .
 
 

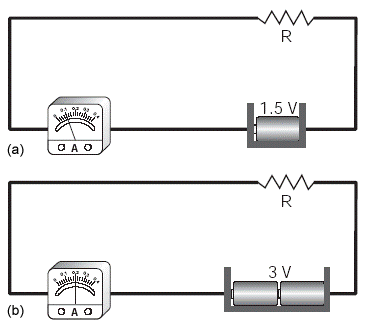
Fig. 4 La resistencia R obedece a la Ley de Ohm.
 

Por tanto, el valor de la resistencia metálica R no se alteró (permaneció constante) al variar el voltaje aplicado. Si continuamos aumentando el voltaje, observaremos que:

  • Triplicando VAB, i también se triplica.


  • Cuadruplicando VAB, i también se cuadruplica, etcétera.

Estos hechos los observó experimentalmente, por primera vez, George Ohm en el siglo XIX, y pueden resumirse en la siguiente ley, que lleva su nombre:
 

Ley de Ohm

La corriente establecida en un conductor metálico es directamente proporcional al voltaje aplicado, de manera que su resistencia permanece constante (no depende del voltaje aplicado).
 
Además de los metales, algunos otros conductores también obedecen la ley de Ohm y por ello se denominan conductores óhmicos. Sin embargo, existen muchos otros conductores que no obedecen esta ley (conductores no óhmicos). En nuestro curso, siempre que nos referimos al valor de una resistencia (por ejemplo, R = 15 ) estamos suponiendo que su valor permanece constante, es decir, que no se altera cuando variamos el voltaje aplicado a la resistencia.
 
Factores que influyen en el valor de una resistencia
 

Para analizar los factores que influyen en el valor de la resistencia de un alambre, consideremos el diseño mostrado en la figura II.16.5: tres hilos de la misma longitud se fijan sobre un soporte de madera, siendo M1N1 y M2N2 hechos del mismo material (una aleación de níquel y cromo) y M3N3, de cobre. Además de eso, M1N1 es más grueso que M2N2 y M3N3, que son iguales entre sí. Hagamos el siguiente experimento.
 
 

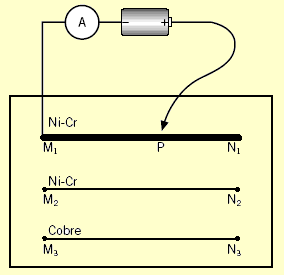
Fig. 5 Montaje que nos permite identificar los factores que influyen en la resistencia eléctrica de un conductor.
 
  1. Uniéndose una pila y un amperímetro A al alambre M1N1 de la forma que se muestra en la figura II.16.5, sólo la resistencia de la porción M1 P será recorrida por la corriente proporcionada por la pila e indicada por el amperímetro. Si desplazamos el contacto móvil P a lo largo de M1N1, aproximándolo a N1, observaremos que la lectura del amperímetro se hace cada vez menor. Como el voltaje de la pila es siempre el mismo, deducimos que la resistencia de la porción M1 P aumenta a medida que aumentamos su longitud. Este experimento nos muestra una propiedad válida para cualquier conductor:
 
La resistencia de un conductor es tanto mayor cuanto mayor sea su longitud.
 
  1. Supón ahora que la pila y el amperímetro fueran conectados a los extremos M1 y N1 y que anotáramos la indicación del amperímetro. Si después esta conexión se hiciera en M2 y N2, es decir, en los extremos del alambre más delgado de níquel-cromo, observaríamos una disminución en la lectura del amperímetro. Por tanto, la resistencia de M2N2 es mayor que la de M1N1. Al acordarnos que esos dos alambres tienen la misma longitud, vemos que difieren sólo en su grosor y llegamos a la siguiente conclusión que es válida para los conductores en general:
 
La resistencia de un conductor es tanto mayor cuanto menor sea el área de su sección transversal, es decir, cuanto más delgado sea el conductor.
 
  1. Conectándose finalmente el amperímetro y la pila a los extremos del alambre de cobre M3N3, veremos que la lectura del amperímetro es mayor que cuando la conexión se hizo en M2N2, es decir, la resistencia del alambre M3N3 es menor que la de M2N2. Como esos alambres tienen la misma longitud y el mismo grosor, concluimos que:
 
La resistencia de un conductor depende del material de que está hecho.
 
Por tanto, algunos materiales son mejores conductores que otros. Por ejemplo, del experimento que acabamos de describir, concluimos que el cobre es mejor conductor que el níquel-cromo. En la tabla siguiente mostramos algunos metales, colocados en orden de la mejor conducción (plata) hacia la peor (níquel-cromo).
 
 
Conexión de resistencias en serie
 

Supón que dos lámparas estén conectadas a una pila de la manera que se muestra en la Fig. 6 (a), de tal forma que haya sólo un camino para que la corriente eléctrica fluya de un polo de la pila hacia el otro: decimos entonces que las dos lámparas están conectadas o asociadas en serie. Evidentemente, podemos asociar más de dos lámparas de esa manera, por ejemplo, en un árbol de navidad, donde generalmente se usa un conjunto de varias lámparas conectadas en serie (Fig. 7). En la Fig. 6 (b) mostramos el diagrama que representa el circuito de la ilustración. Observa la representación de los polos de la pila y de las dos lámparas (resistencias R1 y R2).
 
 
Fig. 6 (a) Circuito de dos focos unidos en serie y conectados a una pila.
 
 
Fig. 6 (b) Diagrama representando el circuito mostrado en la FigI. 6 (a).
 

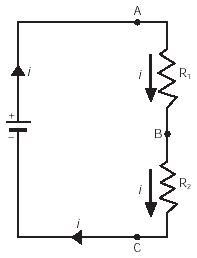
En un conjunto de resistencias en serie, como el de la figura II.16.6, se observan las siguientes características:

  • Como hay un sólo camino posible para la corriente, ésta tiene el mismo valor en todas las resistencias del conjunto (aunque esas resistencias sean diferentes).


  • Es fácil notar que si el circuito se interrumpiera en cualquier punto (en A o B, o en C, en la Fig. 6 (b)), la corriente dejaría de circular en todo el circuito (no hay otro camino para la corriente).


  • Cuanto mayor sea el número de resistencias conectadas en serie, mayor será la resistencia total del circuito (todo pasa como si estuviéramos aumentando la longitud total de la resistencia del circuito). Por tanto, si mantuviéramos el mismo voltaje aplicado al circuito, menor será la corriente establecida en éste.
 
 

Fig. 7 Los focos decorativos en un árbol de navidad generalmente están unidos en serie
 
Conexión de resistencias en paralelo
 

Las dos lámparas de la Fig.8 (a) se conectaron de tal manera que existen dos caminos para el paso de la corriente de un polo de la pila hacia el otro: decimos que las lámparas están asociadas o conectadas en paralelo. Evidentemente, podemos asociar más de dos lámparas (u otros aparatos) en paralelo, abriendo varios caminos para el paso de la corriente (esto sucede, por ejemplo, con los aparatos electrodomésticos). En la Fig. 8 (b), mostramos el diagrama que representa el circuito de la fotografía. En una conexión de resistencias en paralelo, se observan las características siguientes:

  • La corriente total i, proporcionada por la batería, se divide en las resistencias del conjunto (por ejemplo, en la figura II.16.8b, la corriente i se divide en i1 e i2, de manera que i1 + i2 = i). La mayor parte de la corriente i pasará por la resistencia de menor valor (camino que hace menor oposición).


  • Es posible interrumpir la corriente en una de las resistencias del conjunto, sin alterar el paso de corriente en las demás resistencias. Por ejemplo: interrumpiendo el circuito en el punto A de la Fig. 8 (b), la corriente dejará de circular sólo en R1, mientras en R2 la corriente continuará inalterada en su valor i2.


  • Cuanto mayor sea el número de resistencias conectadas en paralelo, menor será la resistencia total del circuito (todo ocurre como si estuviéramos aumentando el grosor de la resistencia del circuito). Por tanto, si mantuviéramos inalterado el voltaje aplicado al circuito, menor sería la resistencia y mayor sería la corriente proporcionada por la pila o batería.
 
 

Fig. 8 (a) Circuito de dos focos unidos en paralelo y conectados a una pila. (b) Diagrama representando el circuito mostrado en la Fig. 8 (a).
 
¿Cómo están conectados los aparatos eléctricos en nuestras casas?
 

Tú sabes que en tu casa, cuando varios aparatos electrodomésticos están en funcionamiento, se puede desconectar uno de ellos y los demás continúan en operación normal. Entonces, tal hecho nos muestra que la conexión de esos aparatos en la red eléctrica de la casa no está hecha en serie, porque si así fuera, la interrupción de la corriente en uno de ellos, como vimos, provocaría que se desconectaran los otros.

En realidad, los aparatos electrodomésticos están unidos en paralelo, como lo muestra la Fig. 9: dos alambres A y B entre los cuales se mantiene un voltaje constante (120 V en algunas ciudades, o 220 V en otras) se instalan a lo largo de la casa y los diversos aparatos son conectados a esos dos alambres en paralelo unos con otros.

En la Fig. 9 vemos, por ejemplo, un enchufe instalado entre D y E; una cafetera, entre F y G; un foco, entre H e I, etc. Observa que:

  • Todos los aparatos están sometidos a la tensión de la red (120 V o 220 V), igual para todos ellos, desconectándose al interruptor del foco, por ejemplo, sólo se apaga éste, sin afectar el funcionamiento de los demás dispositivos.
 
 

Fig. 9 En una casa los aparatos eléctricos están conectados en paralelo.
 
  • Cuanto mayor sea el número de aparatos conectados, menor será la resistencia total del circuito de la casa (como vimos al estudiar el conjunto en paralelo). En consecuencia, mayor será la corriente total que entra en la casa, pasando por el interruptor automático C, que se muestra en la Fig. 9. En la Fig. 10, mostramos un interruptor de ese tipo que, como ya debes haber visto en tu casa, se desconecta automáticamente cuando la corriente sobrepasa un cierto grado de seguridad (por ejemplo: 30 A, 40 A, etc.). La instalación eléctrica de la casa queda así protegida contra un exceso de calentamiento de los alambres.
 
 

Fig. 10 Interruptor automático (o separador), que se desconecta automáticamente cuando la corriente eléctrica a través de él sobrepasa cierto valor.
 
El choque eléctrico
 

Actualmente se sabe que todas las funciones del cuerpo humano se controlan eléctricamente. Por dicha razón, no es de extrañar que una corriente eléctrica, proveniente de una fuente externa (de un tomacorriente, por ejemplo), a través de nuestro cuerpo, pueda causarle problemas. Se observa que nuestra sensibilidad a la corriente eléctrica es muy fuerte, es decir, corrientes relativamente pequeñas pueden causar dolor o incluso la muerte. De hecho, para la mayoría de las personas, se observa que:

  • Una corriente de 0.0001 A, ya es perceptible, causando un cierto “hormigueo”.


  • Una corriente de 0.01 A, puede causar dolores y espasmos musculares, sin ser mortal.


  • Una corriente de 0.1 A, puede causar la muerte porque hace que el corazón palpite de manera irregular y sin coordinación (fibrilación cardiaca).


  • Las corrientes más altas provocan paro cardiaco, daños irreversibles al sistema nervioso y quemaduras intensas, debido al efecto térmico de la corriente.

Consideremos ahora una persona en cuya casa el voltaje de la red eléctrica sea VAB = 120 V y que, accidentalmente, ese voltaje se aplique a su cuerpo (en las puntas de las manos, por ejemplo).

  • Si la piel de la persona estuviera bien seca, la resistencia de su cuerpo sería muy elevada, con un valor R = 100 000 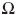aproximadamente. En esas condiciones, de VAB = Ri, tenemos la siguiente corriente a través de la persona:

donde: i = 0.0012 A

Como esa corriente tiene un valor aproximado a i = 0.001 A, la persona sentirá sólo un ligero “hormigueo”.

  • Si la piel de la persona estuviera un poco húmeda (como sucede normalmente debido al sudor), la resistencia de su cuerpo disminuye considerablemente, a un valor de
    R = 10 000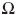 . Entonces, la corriente a través de la persona será:

donde: i = 0.012 A

lo que provocará dolores y espasmos musculares (corriente cercana 0.01 A).
 
 
Fig. 11 (a) Es muy peligroso que una persona con el cuerpo mojado haga contacto con aparatos eléctricos.
 
  • Si los puntos de contacto con los alambres de la red estuvieran mojados, la resistencia del cuerpo se reduce a sólo R = 1 000 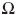(aproximadamente), pues deja pasar una corriente de:

donde: i = 0.12 A

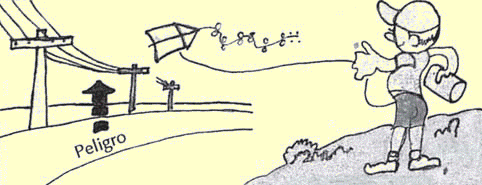
Como vimos, esa corriente generalmente es mortal. Por tanto, al estar con el cuerpo mojado, el contacto, aunque sea con voltajes en casa relativamente bajos, es extremadamente peligroso, (Fig. 11 (a)).

Evidentemente, existe un peligro mucho mayor en dispositivos de alta tensión por producir corrientes más elevadas (cables de transmisión de energía eléctrica, tubo catódico de televisión, nubes en tempestades, etc.) cuyos efectos son aún más desastrosos, según mencionamos anteriormente (Fig. 11 (b)).
 
 
Fig. 11 (b) Volar “papalotes” en las cercanías de un cable de transmisión de energía eléctrica (alta tensión) puede ser fatal.
 
Responda las siguientes preguntas
 
¿Cómo se representa una resistencia en un circuito eléctrico?
 
 
Explique la ley de Ohm.
 
 
¿Cuáles factores y de qué manera afectan a la resistencia eléctrica?
 
 
Describa la conexión de resistencias en serie.
 
 
Describa la conexión de resistencias en paralelo.
 
 
Indique cómo están conectados los aparatos eléctricos en su casa.