Unidad 2. Lectura 2.12
 
Presión en columnas de líquidos.
 

Al introducir una placa de plástico o de cartón, empujada por un tubo, en un recipiente con agua, sentimos resistencia a ser sumergida, pero además la placa no se separa del tubo. Si intentamos empujarla con una vara, notamos que se requiere de cierta fuerza para lograr separarla del tubo. ¿Qué la empuja?, ¿de qué depende ese empuje? Tal vez notemos que la fuerza necesaria para separarla será mayor cuanto mayor sea la profundidad; pero si estamos a una misma profundidad, notaremos que la fuerza es la misma.

Como hemos anotado anteriormente, toda la materia está formada por moléculas, que en los líquidos están en movimiento desplazándose en su interior y colisionando constantemente. Así, si imaginamos la región de agua que está justo debajo de la placa, tendremos una gran cantidad de moléculas golpeándola simultáneamente. El resultado de esas colisiones es una fuerza de empuje que se dirige hacia arriba y que debe superarse para separar la placa del tubo, es decir, moverla hacia abajo (Fig. 1).
 
 

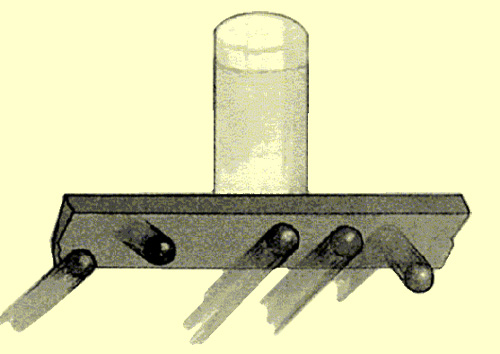
Fig. 1 Las colisiones de las moléculas tienen como resultado una fuerza de empuje hacia arriba sobre la placa.
 
Si ahora introducimos una placa con el doble de área, notaremos que se requiere mayor fuerza para separarla del tubo, lo cual implica que hay más moléculas chocando con la placa. Esto ocurre así siempre en una proporción constante; entre más área, más fuerza de empuje, de manera que:
 
F = PA
 

Donde F es la magnitud de la fuerza de empuje, A el área, y P, que en este caso es la constante de proporcionalidad, es la presión.

De hecho, es común que la presión se exprese por la ecuación:
 
 
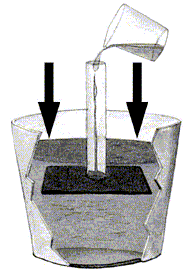
Así, para todo lugar de un fluido a la misma profundidad, la presión será la misma. Esta explicación se aplica al barómetro de Torricelli: las moléculas de la atmósfera ejercen presión sobre el mercurio de la cubeta y mantienen a cierta altura la columna en el tubo cerrado (Fig. 2).
 
 
Fig. 2 Al verter agua en el tubo al mismo nivel que el de la cubeta, las presiones son iguales, por lo que la placa se separará fácilmente.
 

Una forma de separar la placa del tubo sin empujar, consiste en llenarlo con agua; así, al tener la placa encima el mismo nivel de agua, recibirá colisiones tanto por debajo como por arriba, y el resultado neto será una fuerza prácticamente cero (sería cero si el espesor de la placa fuese cero).

Con ello podemos darnos cuenta que la fuerza de empuje es igual a la del peso de la columna de agua, justo encima de la placa, por lo que:
 
F = mg
 
en donde m es la masa del líquido y g es la aceleración de la gravedad. Al sustituir se obtiene:
 
 

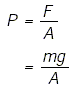
La unidad de presión es N/m2 (newtons/metros cuadrados) en el Sistema Internacional de Unidades, y se le conoce como pascal (Pa). Existen distintos tipos de unidades de la presión; entre las más comunes se encuentran la atmósfera (atm), que equivale a 1.01x105 Pa (este valor corresponde a la presión atmosférica a nivel del mar y se toma como punto de referencia), y los milímetros de mercurio (mm Hg), que equivalen a 1.33x102 Pa.

Para determinar cómo es la relación de la presión con la altura, pensemos en el fondo de un recipiente cuya superficie tiene área A; entonces la presión del líquido en un área estaría dada por el peso del líquido en esa área, es decir:
 
 
 

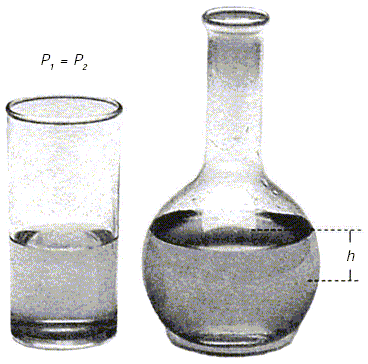
Fig. 3 La presión sólo depende de la profundidad y de la densidad; por eso no importa si el recipiente es delgado o ancho; a la misma profundidad la presión será la misma.
 
Podemos sustituir la masa m en función del volumen del líquido utilizando la expresión:
 
 
que viene de la definición de densidad:
 
 
Sustituyendo la ecuación de la presión tenemos que:
 
 
Como el volumen de un objeto se puede expresar también como el producto del área de la base por la altura (V = Ah), se encuentra finalmente que:
 
P = ρAhg / A = ρgh
 

en donde ρ es la densidad, g es la aceleración de la gravedad y h es la altura de la columna del líquido. Lo mismo ocurre para cualquier lugar del líquido. Lo anterior nos indica que la presión en un área no depende de la cantidad de líquido, sino sólo de su densidad y de la altura de la columna. Por ello, la presión en dos recipientes que tienen distinta área será la misma si la altura de la columna de líquido es la misma.
 

Blas Pascal (1623-1662) supo de los experimentos de Torricelli y, apoyado por los resultados en la construcción del barómetro, se propuso demostrar que el peso del aire era la causa de su funcionamiento y que, por tanto, cambia al variar la altitud. Pascal repitió el experimento de Torricelli en lo más alto del cerro Puy de Dome, cercano a la ciudad de Clermont, Francia, y en el lugar más bajo de la ciudad; encontró que en el punto más alto la columna de mercurio era menor que en el más bajo, indicando que al haber más aire, éste pesa más y, por tanto, la columna es más alta.

Al aceptar que el barómetro funcionaba debido a la presencia de una columna de aire sobre la superficie del recipiente que contenía mercurio, se pusieron al descubierto dos aspectos: que el vacío podía existir en la naturaleza y que el aire era similar al agua, por lo cual podían aplicarse al aire los conocimientos que se tenían sobre la acción del agua en diversos fenómenos.

Torricelli y Pascal utilizaron el concepto de peso del aire sobre la columna de líquido, pues consideraban que este peso empujaba la superficie del líquido fuera del tubo, pero no llegaron a establecer el concepto de presión.