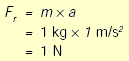Unidad 2. Lectura 2.5
 
La segunda ley de Newton.
 

Una vez que se conocen las características del movimiento cuando no actúa una fuerza o cuando la fuerza resultante es cero, las preguntas que surgen naturalmente son: ¿Qué pasa si la suma de las fuerzas no se anula? ¿Cómo se mueve un sistema sujeto a la acción de una sola fuerza o de una fuerza resultante diferente de cero?

La observación, los experimentos y la reflexión llevaron a Newton a concluir que en estas condiciones la velocidad de un cuerpo no se mantiene constante. Si está en reposo, comenzará a moverse y si está en movimiento, su rapidez o la dirección y sentido de su movimiento cambiará; en pocas palabras, el cuerpo adquiere una aceleración.

Un ejemplo que sirvió a Newton de guía en su análisis fue el de la caída libre de los cuerpos. En este caso la única fuerza que actúa sobre el objeto es su peso, y el movimiento que sigue es uniformemente acelerado.

Newton determinó que la aceleración que adquiere un cuerpo depende tanto de la magnitud, la dirección y el sentido de la fuerza resultante que actúa sobre él, como de la masa del objeto. La fuerza resultante y la masa son las únicas variables involucradas.

La aceleración es directamente proporcional a la magnitud de la fuerza resultante. Así, si se duplica la fuerza, la aceleración se duplica; si se triplica la fuerza, se triplica la aceleración.

Por otro lado, la aceleración es inversamente proporcional a la masa del cuerpo que se acelera. Esto es, a mayor masa, menor aceleración. Si aplicas la misma fuerza sobre dos cajas, una con el doble de la masa que otra, la aceleración de la de mayor masa será sólo la mitad (Fig. 1). La masa resulta ser una medida de la inercia del objeto o de su resistencia a ser acelerado.

La Segunda Ley de Newton resume estas observaciones.
 
 

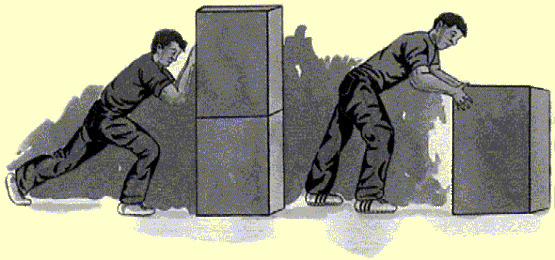
Fig.1 A mayor masa, menor aceleración.
 
La aceleración que adquiere un objeto, sujeto a la acción de una o varias fuerzas, es directamente proporcional a la magnitud de la fuerza resultante que actúa sobre él, e inversamente proporcional a la masa del cuerpo considerado.
 
Si la fuerza resultante se representa como Fr, la masa como m y la aceleración como a, la segunda ley implica que:
 
 
Cuando la fuerza resultante y la masa se expresan en unidades del SI, newtons (N) y kilogramos (kg), respectivamente, la aceleración que resulta tiene unidades de m/s2. Por ejemplo, si al empujar un refrigerador de 250 kg la fuerza resultante sobre él es de 500 N, entonces adquirirá una aceleración de:
 
 
El refrigerador aumentará su velocidad en 2 m/s cada segundo. Como puedes ver, al aplicar una fuerza constante se adquiere una aceleración constante, pero no una velocidad constante. Para que el refrigerador se moviera a velocidad constante, la fuerza resultante sobre él debía ser cero, lo que se logra sólo cuando la magnitud de la fuerza que lo empuja iguala a la de la fuerza de fricción que se opone a su movimiento (Fig. 2).
 
 

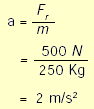
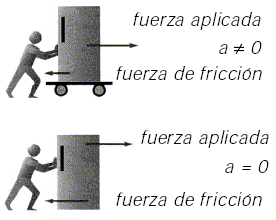
Fig. 2 Relación entre la fuerza aplicada y la fuerza de fricción
 
La segunda ley de Newton también resulta útil para determinar el valor de la fuerza resultante que actúa sobre un cuerpo. Para ello es necesario medir la masa del objeto y la aceleración de su movimiento. La fuerza resultante es entonces igual al producto de la masa por la aceleración:
 
Fr = m × a
 
Si al observar el movimiento de un cuerpo de 1 kg de masa determinas que se acelera a 1 m/s, puedes estar seguro de que la fuerza resultante sobre él es igual a:
 
 
De este ejemplo se deduce una definición más adecuada para la unidad de fuerza llamada newton:
 
Newton es la fuerza que provoca una aceleración de 1 m/s2 en un cuerpo de 1 kg.
 
La segunda ley de Newton establece que la fuerza y la aceleración son directamente proporcionales, pero no hay que olvidar el efecto de la masa. Por ejemplo, cuando un jugador de fútbol patea una pelota de 0.25 kg, es capaz de comunicarle una velocidad de 110 km/h en un centésimo de segundo. Esto equivale a una aceleración cercana a 3000 m/s2. La fuerza de su patada es, entonces:
 
 
En la caída libre cualquier objeto, independientemente de su masa, adquiere una aceleración de 9.8 m/s2. Entonces, si se conoce su masa, puede calcularse la magnitud de la fuerza que actúa sobre él. Si la masa es de 0.1 kg:
 
 
Pero esta fuerza no es otra cosa que el peso del objeto. Como este número es muy cercano a 1 N, ahora puedes entender por qué, de manera aproximada, un newton equivale al peso de un objeto con masa 0.1 kg.