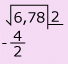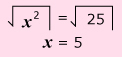Unidad 8 Teorema de Pitágoras Tema 1 Potencias cuadradas
| 23 Evalúa tu masa corporal |
Propósito: Resolverás problemas con potencias cuadradas.
 |
¿Has oído hablar del Índice de Masa Corporal (IMC)? ¿Sabías que el IMC te indica si tienes problemas de sobrepeso o de obesidad? ¿Sabes cómo calcularlo? |
La obesidad es un problema de salud pública que cada vez aumenta. Por ello es importante cuidar la cantidad y calidad de los alimentos que consumimos. El Índice de Masa Corporal se calcula a partir de la talla en metros y del peso en kilogramos de la persona.
| 1) | Verónica leyó la siguiente información en el periódico: |
|---|
Con base en la información anterior, realiza lo que se solicita.
| A) | Escribe la ecuación para calcular el IMC Al utiliza la letra M para representar el IMC, la p para representar el peso y la t para representar la estatura. |
|---|
| B) | Verónica pesa 67 kg y mide 1.52 m, ¿cuál es su IMC? |
|---|
| C) | ¿Verónica tiene problemas de sobrepeso o de obesidad? |
|---|
| 2) | Juanita tiene un IMC de 24.74 y mide 1.57 m, ¿cuánto pesa? |
|---|
| A) | Escribe la ecuación para calcular el IMC, después despeja la p (peso). |
|---|
| B) | Sustituye las medidas de Juanita en la ecuación y calcula su peso. |
|---|
| 3) | Ramón tiene un IMC de 24.38 y pesa 68 kg, ¿cuál es su estatura? |
|---|
| A) | Escribe la ecuación para calcular el IMC y despeja la t2 (estatura al cuadrado). |
|---|
| B) | Sustituye las medidas de Ramón y calcula t2. |
|---|
| C) | ¿Qué dato obtienes? |
|---|
| D) | ¿Qué falta hacer para conocer la estatura de Ramón? |
|---|
| E) | Con la tecla  de la calculadora, calcula la estatura de Ramón. |
|---|
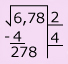
Analiza la forma en que Araceli calcula la medida del lado de la base del siguiente prisma cuadrangular.
| • | Analiza cómo se calcula la raíz cuadrada del número 678. |
||
|---|---|---|---|
Se separan las cifras de dos en dos, empezando por la derecha. |
 |
||
Se busca un número que multiplicado por sí mismo sea igual o casi igual, pero menor, que el número formado por la cifra de la izquierda (6) y se escribe sobre la línea de la derecha. |
 |
||
El número encontrado (en este caso el 2) se multiplica por sí mismo y el resultado se resta del 6. |
 |
||
Dentro de la raíz, se baja el segundo par de cifras. En el exterior, se duplica el número de la primera línea y el resultado se escribe abajo en una segunda línea. |
 |
||
Se busca una cifra (por ejemplo 6) que se agrega a los números de la primera y segunda líneas. La multiplicación de dicha cifra por el número de la línea de abajo (46) debe ser igual o casi igual, pero menor que 278. Se escribe el resultado de la multiplicación y se resta a 278. |
 |
||
El resultado final es 26 y quedan 2. Se comprueba multiplicando 26 por sí mismo y sumando 2: (26) (26) = 676 676 + 2 = 678 |
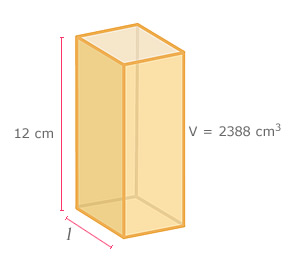
| 4) | El área de un kiosco circular es de 200.96 m2, ¿cuánto mide su radio? |
|---|
| A) | Recuerda que la fórmula para calcular el área del círculo es A = πr2. Despeja r2 de la fórmula. |
|---|
| B) | Sustituye los valores y encuentra el valor de r2. Toma 3.14 como valor de π. |
|---|
| C) | ¿Qué falta para conocer el valor de r? |
|---|
| D) | Haz la operación necesaria y escribe cuánto mide el radio. |
|---|
| 5) | Van a poner una serie de focos alrededor de un kiosco circular cuya superficie mide 271.57 m2. ¿Cuál es la medida mínima que debe tener la serie para que al menos le dé una vuelta completa? |
|---|
| A) | Despeja r2 de la fórmula A = π r2 |
|---|
| B) | Sustituye los valores y encuentra el valor de r2. Tomar 3.14 como valor de π. |
|---|
| C) | ¿Qué falta para conocer el valor de r? |
|---|
| D) | ¿Cuánto mide el radio? |
|---|
| E) | ¿Cuál es la medida del diámetro del círculo? La fórmula para calcular el perímetro de un círculo es P = π d |
|---|
| E) | ¿Cuál es la medida mínima que debe tener la serie? |
|---|
| 6) | Calcula el valor de la incógnita de las siguientes ecuaciones. |
|---|
| A) | l2 + 9 = 1 333.96 l=
|
|---|
| B) | m2 – 10 = 28.44 m =
|
|---|
| C) | 100 p2 = 334.08 p =
|
|---|
| D) | 
|
|---|
