circulo Unidad 7 Monomios y polinomios circulo Tema 2 Suma y resta de Monomios y Polinomios circulo

21 Carpetas

 

 

Propósito: Sumarás y restarás monomios y polinomios.

Propositos ¿Consideras a los trabajos manuales como un arte o simplemente como una actividad más?, ¿conoces alguien que borde, teja y elabore carpetas?

El trabajo manual que muchas mujeres realizan en nuestro país, como el bordado, el deshilado y el tejido que en muchas ocasiones llegan a ser verdaderas obras de arte, es poco apreciado y, generalmente, pobremente remunerado.

 

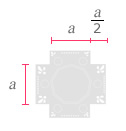
1)
Gelita y sus amigas elaboran carpetas de formas poco comunes como las que se muestran en las figuras 1 y 2.

 

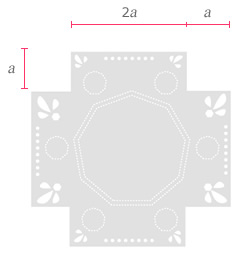
mantitamantita 2

A)
¿Cuántos lados de la figura 1 miden a?


 

¿Cuántos lados miden 2a?


 

B)
¿Cuánto mide el perímetro de la figura 1?


 

C)
¿Cuántos lados de la figura 2 miden a?


 

¿Cuántos lados miden ?


 

D)
¿Cuánto mide el perímetro de la figura 2?


 

E)
¿Qué cantidad de encaje es necesaria para adornar ambas carpetas?


 

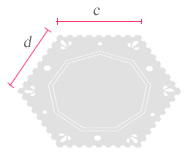
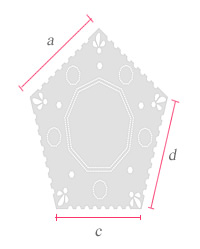
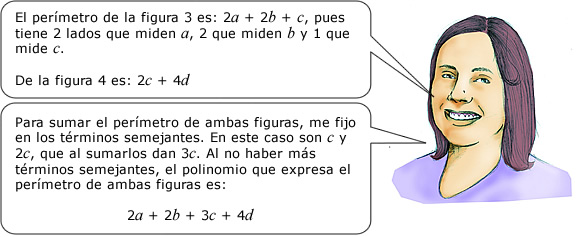
Analiza el procedimiento de Gelita para saber la cantidad de encaje que necesita para adornar las carpetas representadas con las siguientes figuras.

mantita_3mantita

act_18_2


resolvamos

2)
Si requieres escribir una literal con exponente, escribe la literal, después haz clic en exponente y escribe el número que necesites como exponente.


A)
Explica por qué 45xy y xy son términos semejantes.


 

B)
Explica por qué 8bc y 8ab no son términos semejantes.



 

C)
Explica por qué 26m2n y 10mn2 no son términos semejantes.



 

D)
Explica por qué 8a2bc y 2ca2b son términos semejantes.


 

3)
Une los términos semejantes de las columnas Haz clic en el término de la columna de la izquierda y después en el término semejante en la columna de la derecha. Para modificar tu respuesta haz clic en la línea que deseas borrar y después en limpiar.

 

A veces los polinomios están dentro de un paréntesis. Dicho paréntesis puede estar antecedido por un signo de más o de menos (+ o –).

Eliminación de paréntesis
 

•

Si el signo que le antecede al paréntesis es positivo, se quita el paréntesis sin cambiar el signo de los sumandos del polinomio dentro del paréntesis.

Ejemplo:

(2n+ 4n) + (45mn – 7mn2 + 8n)
2n+ 4n + 45mn – 7mn2 + 8n

Reduciendo o simplificando términos semejantes tenemos:

14n+ 45mn– 7mn2
   

•

Si el signo que le antecede es negativo, se multiplica por –1 cada sumando del polinomio, dentro del paréntesis. Con esto cambiará el signo de cada sumando y se quitará el paréntesis.

Ejemplo:

2n+ 4n) – (45mn – 7mn2 + 8n)
2n+ 4n – 45mn + 7mn2– 8n

Reduciendo o simplificando términos semejantes:

–2n – 45mn + 7mn2
   

•

Cuando un paréntesis lleva signo positivo y está al inicio del polinomio, generalmente no se escribe el signo, pero si es negativo, sí se escribe:

Ejemplo:

– (2n+ 4n) – (45mn– 7mn2 + 8n)
–2n– 4n – 45mn+ 7mn2– 8n
Reduciendo o simplificando términos semejantes:

–14n– 45mn + 7mn2
   

•

Cuando hay varios paréntesis unos dentro de otros, se eliminan paso a paso, iniciando con los interiores.

Ejemplo:

– (2n + 4n) – [– (9mn + 15n) + (45mn– 7mn2 + 8n)]
– (2n + 4n) – [–9mn – 15n + 45mn – 7mn2 + 8n]
–2n – 4n + 9mn + 15n – 45mn + 7mn2– 8n

Reduciendo o simplificando términos semejantes tenemos:

n – 36mn + 7mn2
   


4)
Para escribir una literal con exponente, escribe la literal, después haz clic en exponente y escribe el número que necesites como exponente.

 

area area 2


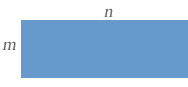
A)
Perímetro del rectángulo.


 

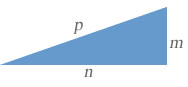
B)
Perímetro del triángulo.


 

C)
Suma de ambos perímetros.


 

5)
Reduce los siguientes polinomios. Para escribir una literal con exponente, escribe la literal, después haz clic en exponente y escribe el número que necesites como exponente.

 

A)
7n – 2n + 4n – 3m =


 

B)
2y2 + 2x3– 9y2– x =


 

C)
5y2 + 3y + y2 – 2y =


 

D)
4ab2– 7x3y + 9ab2 + x =


 

E)
3x2y + 8x3y – 4x2y =


 

F)
9p2 + x3y + 2y2– x =


 

6)
Suma o resta los siguientes polinomios. Para escribir una literal con exponente, escribe la literal, después haz clic en exponente y escribe el número que necesites como exponente.

 

recuerda que...