Operaciones avanzadas

Unidad 3 Expresiones algebraicas Tema 1 Uso de las literales

8 El trabajo de don Chuy

Propósito: Conocerás la utilidad de las literales en el álgebra. Usarás algunas reglas de escritura algebraica.

¿Has sembrado árboles?, ¿has tenido problemas para regarlos y cuidarlos? Comenta con un familiar o con tu asesor.

Como todo trabajo, el cuidado de los árboles es algo que se puede optimizar, es decir, que al hacerlo se puede ahorrar tiempo y esfuerzo.

1)	Sembraron 35 árboles en hilera con igual separación uno del otro. Don Chuy pidió un tinaco con agua para regar uno a uno con una cubeta. Don Chuy quiere caminar lo menos posible al regarlos. ¿Dónde tiene que colocar el tinaco, junto al árbol de en medio o junto a un árbol de cualquier extremo?

A)	¿Por qué?

B)	Si hubieran sido 36 árboles, ¿cuál hubiera sido el lugar ideal para colocar el tinaco?

Sugerencias: Supón una menor cantidad de árboles. Determina una distancia igual entre cada árbol.

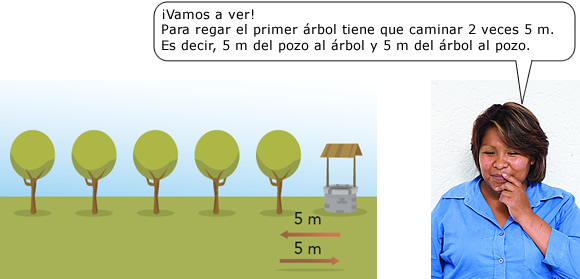
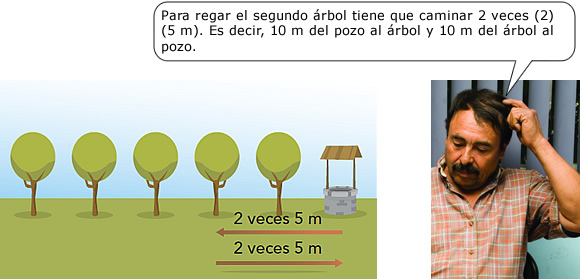
Analiza los razonamientos de Sonia y Miguel ante una situación parecida.

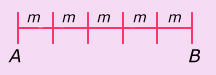
Se sembraron árboles en hilera. La distancia entre cada árbol es de 5 m. Sobre la misma hilera y a 5 m del primer árbol hay un pozo, ¿cuántos metros tiene que caminar don Chuy para regar con una sola cubeta cada árbol?

act_8_1_textos

act_8_2_textos

act_8_1_textos

2)	Observa a tu alrededor y localiza objetos con forma rectangular.

A)	Considera que el siguiente rectángulo representa cualquiera de las formas rectangulares que viste. La letra l representa el largo del rectángulo y la letra a el ancho. Escribe cada letra en el recuadro que le corresponde en la figura.

B)	¿Cuál es el perímetro del rectángulo?

3)	Observa que los siguientes objetos rectangulares de papel tienen el mismo tamaño y colocados uno junto a otro forman un rectángulo cuyo largo se representa con la letra b.

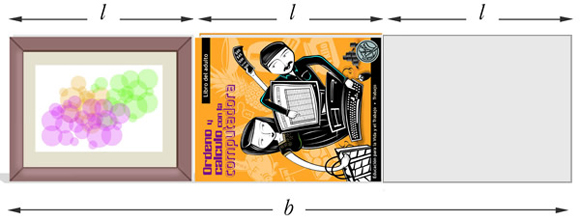
act_8_2

A)	El largo de cada objeto mide l. Utiliza l para representar la medida b:

B)	¿Cuál es el perímetro si el ancho del rectángulo formado por los tres objetos mide a?

C)	Si el valor de l es 37 cm y el de a es 21 cm, ¿cuánto mide el perímetro del rectángulo formado?

4)	El peso de cada chocolate confitado es b, ¿cuánto pesa un sobre si trae 55 chocolates?

5)	El precio del dólar varía con mucha frecuencia. Utilizando una letra, ¿cómo puedes representar el importe de 250 dólares?

•	En álgebra se usan letras para representar cantidades y se les llama literales. Ejemplo En este caso, la literal es m y representa la medida del segmento.

•	Su empleo es parecido al de los números en la aritmética. Ejemplo. Como cada segmento pequeño mide m, la medida del segmento AB es: m + m + m + m + m = 5m

	Lo anterior es porque la multiplicación por un número y una literal o entre dos literales, se expresa escribiendo juntos el número y la literal, o las dos literales juntas. 5m expresa una multiplicación de 5 por m.

6)	Un auto recorrió la distancia AB en un día. El día siguiente recorrió la distancia BC, como se indica en el siguiente diagrama.

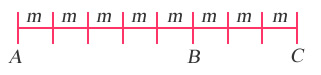
act-8_3

A)	Utiliza la literal m para expresar la distancia que recorrió en los dos días.

7)	La medida de la altura de un escalón es u, ¿qué significa 8u?

A)	Escribe 8u como suma.

8)	La siguiente figura muestra las distancias recorridas por un ferrocarril.

¿Qué distancia hay de A a B?

¿Cuál es la distancia de B a C?

¿Cuál fue la distancia total del recorrido?

•	Expresiones como se conocen como expresiones algebraicas.

•	Las expresiones algebraicas están formadas por un coeficiente, una literal o literales (letras) que están elevadas a algún exponente y signos de operaciones.

•	Coeficiente: Es el número que multiplica una literal. Ejemplo. 5 es el coeficiente de la expresión 5m

•	Cuando dos expresiones algebraicas tienen la misma literal o literales y éstas están elevadas al mismo exponente, se dice que son términos semejantes. Ejemplo. 5m³ es semejante a 3m³.

•	Dos términos semejantes se pueden simplificar. Ejemplos. 5m + 3m = 8m –9b + 7b = –2b

•	Cuando dos expresiones algebraicas tienen diferente literales o diferente exponente, que no son términos semejantes. Por ejemplo. 7n no es semejante a 9t

•	Cuando dos términos no son semejantes no se simplifican. Ejemplos. 7n + 9t 5n + 6t – 2n + 8n = 11n + 6t

9)	Haz clic en siguiente y simplifica las siguientes expresiones algebraicas.

10)	Sembraron 5 árboles en hilera con igual separación uno del otro. Don Chuy pidió que colocaran un tinaco con agua junto al primer árbol para regar uno a uno con una cubeta. Escribe la expresión para calcular la distancia que va a caminar don Chuy si la distancia entre árbol y árbol es l, si regresa al tinaco.

A)	Si l mide 1 m, ¿cuánto caminará don Chuy?

B)	Si l mide 2 m, ¿cuánto caminará don Chuy?

C)	¿Qué distancia hay entre árbol y árbol si don Chuy camina 120 m?

11)	Diego gana una comisión f por cada $100.00 que venda. Hoy vendió $900.00, ¿cuál fue su comisión? Escribe una expresión algebraica.

A)	Si f vale $3.00, ¿cuánto dinero le dieron de comisión?

B)	Si f valiera $5.00, ¿cuánto tendrían que darle de comisión?

12)	Observa la siguiente figura.

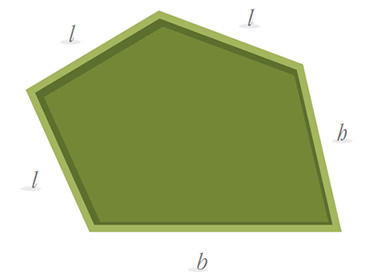
act_8_5

A)	¿Cuál es el perímetro de la figura? Escribe una expresión algebraica.

B)	Si l vale 9 m, h vale 11 m y b vale 13 m, ¿cuántos metros mide el perímetro?

13)	Haz clic en siguiente y calcula el valor numérico de las siguientes expresiones algebraicas.

Consideras que: b = 12, l = 20, d = 5, h = 30, m = 1 para calcular.

14)	La siguiente tabla que muestra las fórmulas para calcular la cantidad de kilocalorías diarias que debemos consumir. Analiza y responde.

Tipo de actividad	Hombres	Mujeres
Ligera	(11.6p + 879) 1.55	(8.7p + 879) 1.56
Moderada	(11.6p + 879) 1.78	(8.7p + 879) 1.56
Intensa	(11.6p + 879) 2.1	(8.7p + 879) 1.82

p representa el peso de la persona en kilogramos.

A)	¿Cuántas kilocalorías debe consumir Pablo al día si pesa 67 kg y tiene una actividad intensa?

B)	Lucía realiza una actividad intensa y pesa 63 kg. ¿Cuántas kilocalorías debe consumir?

C)	Calcula las kilocalorías que deben consumir tu esposo o esposa, tu asesor o asesora y tú.