![]() Unidad 3 Expresiones algebraicas
Unidad 3 Expresiones algebraicas ![]() Tema 3 Uso del lenguaje algebraico
Tema 3 Uso del lenguaje algebraico ![]()
| 10 La experiencia hace la diferencia |
Propósito: Utilizarás el lenguaje algebraico. Modelarás con expresiones algebraicas algunas situaciones de la geometría y de la física.
| ¿Alguna vez has realizado un experimento?, ¿aprendiste algo al realizarlo? |
Los experimentos son fuente de conocimiento. La mayoría de los conocimientos científicos han surgido a partir de experimentar una y otra vez y las matemáticas juegan un papel muy importante en ellos pues permiten cuantificar y modelar distintos fenómenos.
| 1) | ¿Sabes cómo varía la longitud de una liga al colocar en uno de sus extremos diferentes pesos? |
|---|
Para contestar esta pregunta sigue las indicaciones y realiza el siguiente experimento.
| A) | Consigue los siguientes materiales: |
|---|---|
• una liga • 48 canicas de vidrio del mismo tamaño y peso • una bolsa de plástico con capacidad para las 48 canicas • dos clips mariposa • una regla graduada |
| B) | Abre un poco los clips y cuelga en uno la liga por uno de sus extremos. En el otro extremo coloca el otro clip, como se muestra en la siguiente ilustración. |
|---|
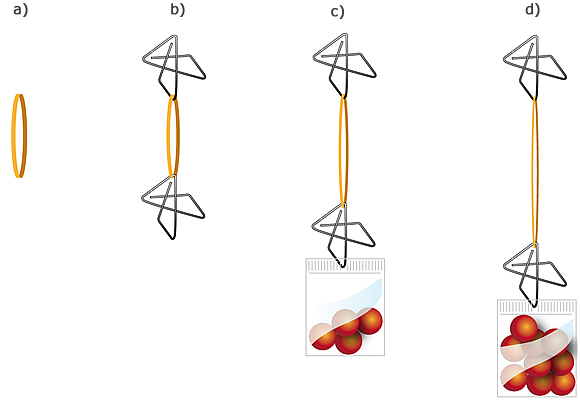
| a) | Mide la longitud de la liga. Escribe tu medida en la tabla. |
|---|---|
b) |
Sujeta la liga por uno de los clips, y en el otro extremo coloca el otro clip. |
| c) |
Coloca peso 8 canicas en la bolsa de plástico y colócala en el otro clip. Mide el largo de la liga y registra tu medición.
|
| d) | Duplica el peso (pon 8 canicas más) en la bolsita. Vuelve a medir la liga y registra el resultado. |
| e) | Triplica el peso de la bolsita y repite la operación tres veces más, agregando cada vez 8 canicas. Registra el resultado de tus mediciones. |
Paso (p) (número de canicas) |
0 |
||||
Largo en centímetros |
| C) | ¿Cómo cambia l con respecto a p? |
|---|
| D) | ¿Cuál es la fórmula que permite calcular l a partir de conocer p? |
|---|
| E) | Investiga en internet cómo se le llama, en Física al fenómeno anterior. |
|---|
| 2) | Escribe la expresión algebraica que representa cada una de las expresiones siguientes, observa el ejemplo. |
|---|
| 3) | Marina compró un terreno rectangular de 200 metros cuadrados. Ella puede elegir las dimensiones de acuerdo con sus necesidades. Si quiere que las dimensiones del terreno sean metros enteros, ¿cuáles son las dimensiones que el terreno puede tener? |
|---|
| A) | Completa la tabla con las medidas que puede tener el terreno. |
|---|
Largo (l) metros |
200 |
100
|
50
|
40
|
20
|
Ancho (a) metros |
| B) | Haz clic en la fórmula que permite encontrar el ancho a partir del largo. |
|---|
| 4) | Consigue el siguiente material: |
|---|---|
• Varios objetos en forma de cilindro. • Una cinta métrica. |
| A) | Mide el diámetro de la base de cada objeto y el perímetro de la circunferencia. Después registra los datos en la tabla siguiente. |
|---|
Longitud del diámetro en cm (d) |
|||||
Perímetro de la circunferencia en cm (C) |
| C) | Divide el perímetro de cada circunferencia entre la longitud del diámetro correspondiente. |
|---|
| D) | ¿Es constante en todos los casos? |
|---|
| E) | Haz clic en la fórmula para calcular el perímetro de la circunferencia a partir de la longitud del diámetro. |
|---|
| 5) | Realiza lo siguiente. |
|---|
| • | Toma un palo largo y mídelo con una cinta métrica. |
|---|---|
| • | Haz una marca en la mitad. |
| • | En un extremo cuelga un kilogramo de algo (una pesa, frijol o maíz). |
| • | Cuelga en el otro extremo dos kilogramos de algo. |
| • | Coloca el palo sobre una base de modo que los pesos queden suspendidos. La base debe quedar debajo de la marca que hiciste en el palo. |
| A) | ¿Qué sucede? |
|---|---|
| B) | Busca la manera de ponerlo en equilibrio sin quitar peso de ningún lado. |
| C) | ¿De qué manera puedes lograrlo? |
| D) | ¿Cuál es la distancia entre el objeto que pesa un kilogramo y el punto de apoyo? |
| E) | ¿Cuál es la distancia entre el peso de 2 kilogramos y el punto de apoyo? |
Escribe los resultados en la siguiente tabla.
| Peso del objeto (p) | (p1) 1 kg |
(p2) 2 kg |
| Distancia (d) | (d1) |
(d2) |
¿Cómo puedes conocer d2 a partir de conocer las otras tres cantidades?
| 6) | Analiza la siguiente tabla, que contiene medidas de cuadrados. Complétala y realiza lo que se indica. |
|---|
Largo (l), centímetros |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Área (A), centímetros cuadrados |
1
|
4
|
9
|
16
|
36
|
| A) | ¿Al duplicar la medida del lado de un cuadrado, su área se duplica? ¿Qué sucede con el área respecto al área inicial? |
|---|
| B) | A continuación, en la imagen del lado izquierdo se representa un geoplano en el que se ha dibujado un cuadrado de 1 cm2 de área. En el geoplano del lado derecho se representa un cuadrado de 9 cm2 de área. Analiza ambos dibujos. |
|---|
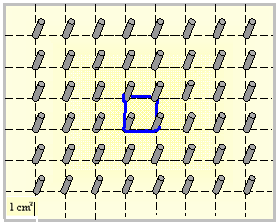

| C) | ¿Al triplicar la medida del lado del cuadrado del inciso a), su área se triplica? ¿Qué sucede con el área respecto al área inicial? |
|---|
¿Qué sucede con el área respecto al área inicial?
| D) | ¿Qué pasa con el área del cuadrado del inciso a) al cuadriplicar y quintuplicar la medida de sus lados? |
|---|
| E) | Escribe la fórmula para calcular el área de un cuadrado. |
|---|
| F) | Analiza los datos de la siguiente tabla y complétala. |
|---|
Lado (l) |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
Área (A) |
25 |
100 |
225 |
400 |
625 |
900 |
1225 |
25(2)(2) |
25(3)(3) |
25(4)(4) |
| G) | Óscar escribió las cantidades que aparecen en la última fila de la tabla renglón porque dice que si se duplica la medida de los lados de un cuadrado, el área original se multiplica por 22; si se triplica la medida de los lados, el área original se multiplica por 32; cuando se cuadriplica la medida de los lados, el área original se multiplica por 42 y así sucesivamente. ¿Tiene razón? |
|---|
| H) | Una lona que mide 4 m de ancho por 6 m de largo cuesta $234.00, ¿cuánto costará una lona de la misma calidad que mide 8 m × 12 m? |
|---|
| I) | Al aumentar el diámetro de un círculo al triple, ¿cuánto aumenta su área? |
|---|
| 7) | Analiza los datos de la siguiente tabla en la que aparecen los volúmenes de algunos cubos. Complétala y realiza lo que se indica. |
|---|
Arista (l) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Volumen (V) |
1 |
8 |
27 |
125 |
343 |
| A) | Al duplicar la medida de la arista de un cubo, ¿qué sucede con el volumen respecto al volumen del cubo inicial? |
|---|
| B) | Dibuja en tu cuaderno un cubo de arista 1cm y un cubo de arista 2 cm. |
|---|
Entra al Foro y haz comentarios sobre las actividades que desarrollaste en esta unidad. Expón tus dudas y analiza las aportaciones de otras personas.
Haz clic en Foro.