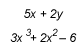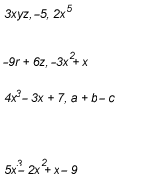UNIDAD II BLOQUE B Actividad 28

BLOQUE B: SISTEMAS DE ECUACIONES

Propósito: Utilizará operaciones con polinomios y simplificará términos semejantes.

 

 

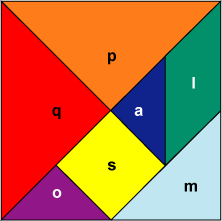  Una diseñadora de mosaicos en acrílico quiere saber qué cantidad de material de cada color necesita para construir un mosaico como el anterior. Para averiguarlo, ha diseñado una unidad de medida.

 

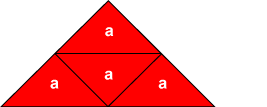
La unidad de medida que quiere utilizar es la siguiente: Observe que a esa unidad de medida la llamó a:

La unidad de medida a cabe 4 veces exactamente en el triangulo rojo, por lo que se necesita:

              
a + a + a + a = 4a

Es decir, cuatro veces la medida a de acrílico rojo.

Observe que el mosaico está formado por 7 figuras en total y dos se repiten, así que son cinco figuras de diferentes formas.

 
 
 

 

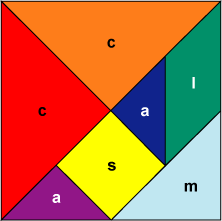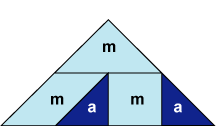
Aunque usted puede observar que l, m y s son figuras diferentes, éstas tienen áreas iguales.

Por lo anterior podemos indicar que el área del mosaico esta formado por:

Agrupando términos semejantes tenemos:

A expresiones como la anterior se les llama trinomios porque constan de tres términos.

 

¿Cómo podría usted expresar con letras y números el área de la siguiente parte del mosaico?

El área de esa parte del mosaico la podemos expresar como:

o como:

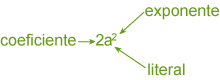
Hasta el momento hemos utilizado tres nombres para identificar a las expresiones algebraicas con las que nos hemos encontrado: Ejemplos:

Seguramente usted recordará que toda expresión algebraica consta de un coeficiente, una parte literal y un exponente.

Queremos aclararle que los binomios y los trinomios también reciben el nombre de polinomios. En general, un polinomio es una expresión algebraica que consta de dos o más términos.

Ejemplos de polinomios:

Los términos en una expresión algebraica comúnmente se separan con el signo más o menos, pero no con un signo de multiplicar, un paréntesis o una línea que indique división.


Ejemplos:

 

Monomios

Binomios

Trinomios

Polinomios

Polinomios de
cuatro términos


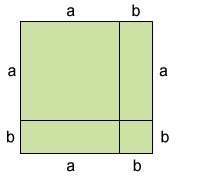
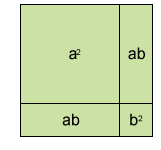
Calcule el área de la siguiente figura:


El área del cuadrado se puede conocer sumando las áreas de cada una de las figuras que lo integran.



Pero como los términos ab y ab son semejantes, podemos sumarlos. De tal modo que el área del cuadrado se puede representar con el polinomio:

 

Calcule las áreas de las siguientes figuras y escriba el frente de cada expresión si ésta es un monomio, un binomio, un trinomio o un polinomio.
 
  Presione el botón "imprimir". Obtenga la hoja impresa y realice ahí su ejercicio. Consérvelo en su carpeta.