UNIDAD II BLOQUE A Actividad 17

BLOQUE A: ECUACIONES LINEALES

Propósito: A partir de la idea de equilibrio en la balanza, usted resolverá ecuaciones lineales.

 

	La señora Jovita es propietaria de una procesadora de aceitunas llamada Los Olivos. Le acaban de surtir barricas de varios tamaños que contienen aceitunas. Para distinguir las barricas, a cada una le asignó una letra: a la chica, le llamó a, a la mediana b y a la grande c.
	Arrastre con el mouse al plato de la balanza las pesas necesarias para equilibrarla.
	Presione en el inciso que expresa el peso de la barrica con aceitunas más grande.
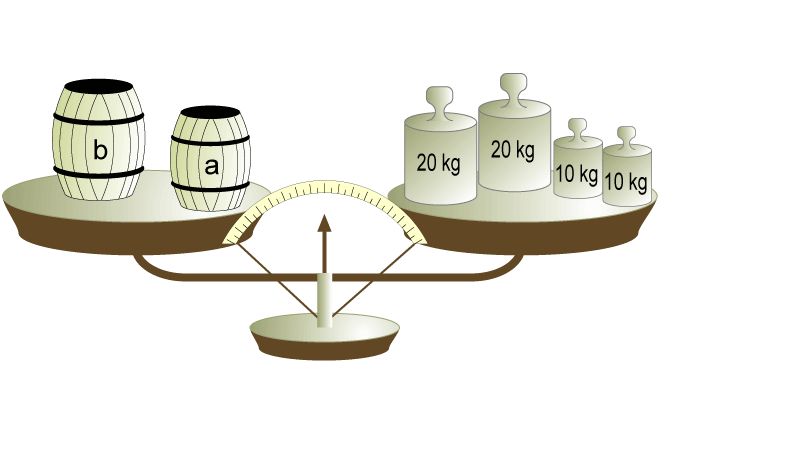
	Observe la siguiente ilustración. Presione en el inciso que represente la situación de la balanza.
	Ahora vamos a resolver los siguientes problemas. Todos ellos se refieren a la ilustración anterior. Si sabemos que el peso de la barrica b es de 40 kg, ¿cuánto pesa la barrica a? Usted puede encontrar el peso de la barrica con aceitunas usando algún procedimiento que se le ocurra. Por ejemplo: • Observar la balanza y hacer algunas operaciones mentalmente.     • Otra manera más sistemática para conocer el peso de la barrica es plantear la ecuación correspondiente y resolverla:     40 + a = 60 En la ecuación anterior: a es la incógnita, es decir, es el valor que se desconoce.     • Para encontrar el valor de a, considere esta ecuación como una balanza en equilibrio, en donde en cada platillo podemos agregar o quitar la misma cantidad para no alterar el equilibrio.
	En la ecuación 40 + a = 60, ¿cómo podemos quitar del lado izquierdo del signo igual (=) el número 40, sin que se pierda el equilibrio? Restamos 40 en el miembro izquierdo de la igualdad y restamos 40, en el miembro derecho, para que se conserve la igualdad, esto es: 40 – 40 + a = 60 – 40        a = 20 Significa que el peso de la barrica a es de 20 kg.
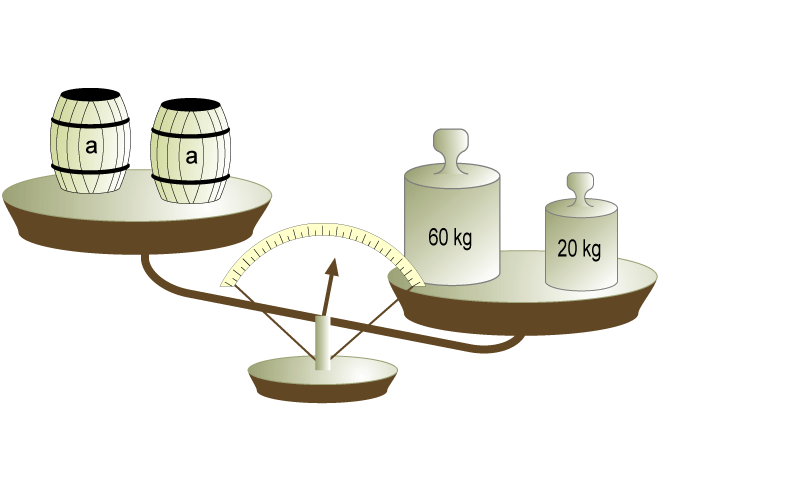
	Veamos la siguiente balanza y considere que ya conoce el valor de "a", el cual es igual a 20 kg:
	A	¿Cuántos kilogramos le faltan al platillo de la izquierda para igualar el peso del platillo de la derecha?

	Presione el botón "imprimir". Obtenga la hoja impresa y realice ahí su ejercicio. Consérvelo en su carpeta.
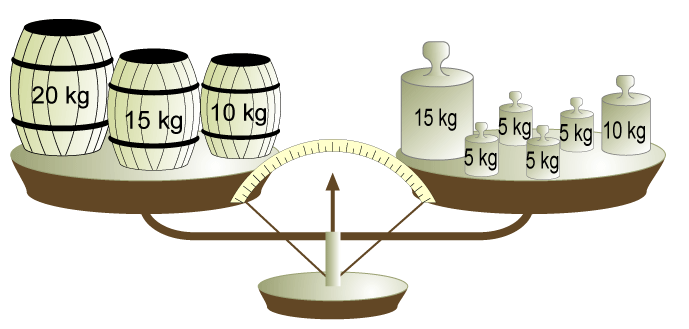
	Tome en cuenta los pesos de las barricas con las aceitunas:

Presione el botón "comparar" y coteje sus respuestas. Si es el caso, realice las correcciones necesarias. Conserve esta impresión, guárdela en su carpeta. Para que una balanza se encuentre en equilibrio, es necesario que el peso en los dos platillos sea el mismo. Por ejemplo: Si aumentamos 15 kg. en un platillo, debemos aumentar 15 kg en el otro platillo, de esta manera el equilibrio de la balanza se mantiene. En una igualdad ocurre lo mismo, por ejemplo: 20 + 10 = 5 + 5 + 5 + 5 + 10 30 = 30 Para que la igualdad se conserve:

Si aumentamos 15 en el miembro de la izquierda, debemos aumentar 15 en el miembro de la derecha:		Si quitamos 20 en el miembro de la izquierda, debemos quitar 20 en el miembro de la derecha:
30 + 15 = 30 + 15 45 = 45		30 – 20 = 30 – 20 10 = 10

El modelo de la balanza nos sirve para entender cómo se resuelven las ecuaciones. Si a un miembro de la igualdad le sumamos o restamos algún número, hay que sumarlo o restarlo en el otro miembro para mantener la igualdad.

Resuelva los problemas siguientes. Primero soluciónelos mentalmente y después, escriba en los rectángulos las ecuaciones, usando lenguaje algebraico, es decir, literales y números. Utilice la información: Barrica a con aceitunas = 20 kg Barrica b con aceitunas = 40 kg Barrica c con aceitunas = 60 kg Ejemplo: a) En un día la señora Jovita vendió cuatro barricas de aceitunas del tamaño a y tres del tamaño b. ¿Cuántos kilogramos de aceitunas vendió? Resuelva el problema con el lenguaje algebraico:         4a + 3b = x      4(20) + 3(40) = x             80 + 120 = x                          x = 200

	Presione el botón "comparar" y coteje sus respuestas. Si es el caso, realice las correcciones necesarias. Presione el botón "comparar" y coteje sus respuestas. Si es el caso, realice las correcciones necesarias.
	Presione el botón "imprimir". Obtenga la hoja impresa y realice ahí su ejercicio. Consérvelo en su carpeta. Ahora resuelva las ecuaciones propuestas

Presione el botón "comparar" y coteje sus respuestas. Si es el caso, realice las correcciones necesarias.

• Una ecuación es una igualdad compuesta por dos miembros, en la que se presenta por lo menos un valor desconocido llamado incógnita. Por ejemplo:                                                                  c – 10 = 50 En este ejemplo, la incógnita es la literal c. • Una ecuación con una incógnita se llama lineal o de primer grado si la incógnita aparece elevada a la primera potencia:                                                                       c1 = c