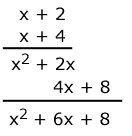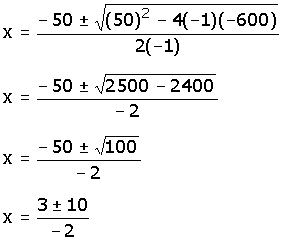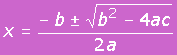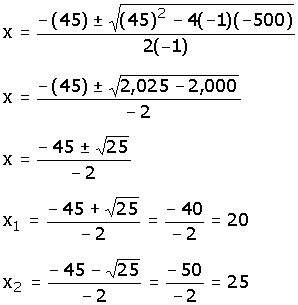Agapito plantea sus ecuaciones de la siguiente manera:
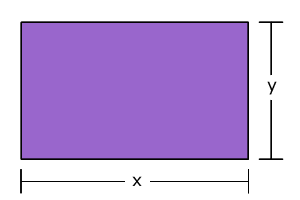 |
| Como el área de un rectángulo se obtiene multiplicando la longitud de sus lados, se puede plantear la siguiente ecuación: |
| x • y = 600 |
Como el perímetro de un rectángulo es igual a la suma de todos sus lados, se puede plantear la siguiente ecuación:
| x + x + y + y = 100 |
Simplificando la ecuación se tiene:
| 2x + 2y = 100 |
y dividiendo entre dos ambos términos se tiene:
| x + y = 50 |
Con esto, Agapito tiene dos ecuaciones y dos incógnitas:
| x • y = 600 -------------- (1)
x + y = 50--------------- (2) |
Procede a resolver sus ecuaciones simultáneas, despejando una incógnita de una de las dos ecuaciones y sustituyéndola en la otra.
| x + y = 50 y = 50 - x |
Sustituye el valor de "y"=50 - x en donde se encuentra la "x" de la primera ecuación.
| x • y = 600 x (50-x)= 600 50x - x2 = 600 |
Multiplicando por -1 ambos términos se tiene:
| -1 • (50x - x2) = -600 |
Ahora conviene reordenar para tener las formas de una ecuación cuadrática:
| x2 - 50x + 600 = 0 |
Observe que la ecuación se ordena expresando los elementos de mayor a menor exponente .

Con lo anterior, Agapito tiene una ecuación con una x2 . A este tipo de ecuaciones se les llama cuadráticas o de segundo grado, porque el exponente más alto que hay en ella es un cuadrado.
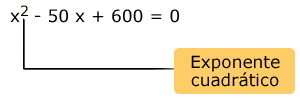
Este tipo de ecuaciones tienen una incógnita (x) pero dos soluciones. Es decir, que existen dos valores de x que satisfacen la ecuación.
Si observa usted esta ecuación con cuidado, se dará cuenta que tiene la forma de un trinomio (x2 + bx + c ) que se obtiene del producto de sus factores: (x + f)(x + q)
donde:
| b = p + q c = p • q |
Una ecuación cuadrática de la forma ax2 + bx + c = 0 se resuelve por factorización o aplicando la fórmula cuadrática (esta última la veremos más adelante).
Factorizar una expresión significa escribir la expresión como producto de sus factores, asi por ejemplo:
| x2 + 6x + 8 = 0 |
Se puede escribir como producto de sus factores (x+2) y (x+4)
|
|
| (x + 2)(x + 4) = x2 + 6x + 8 |
Observe que el coeficiente de x es la misma de 2+4=6 y que la constante 8 es el producto de 2 • 4.
Así entonces, para factorizar una expresión de la forma x2 + bx + c se necesita encontrar dos números cuya suma sea igual a b y su producto igual a c.
Factorizar la ecuación
| x2 - 50x + 600 = 0 |
significa encontrar dos números cuya suma de -50 y su producto sea igual a 600 como el coeficiente de x es negativo (-50) entonces los dos números deben ser negativos para que su producto de positivo (600).
Hagamos una lista de números (negativos) cuyo producto sea igual a 600.
| factores de 600 | suma de factores |
( -60 ) ( -10 ) ( -30 ) ( -20 ) |
( -60 ) + ( -10 ) = -70 ( -30 ) + ( -20 ) = -50 |
como el producto de (-30) por (-20) es igual a 600 y la misma de -30 y -20 es igual a -50, netonces los números que buscamos son: -30 y -20
Así entonces la ecuación
| x2 - 50x + 600 = 0 |
se puede expresar como producto de sus factores
| x2 - 50x + 600 = (x-30)(x-20) |
Observando sus factores determinamos que la ecuación
| x2 - 50x + 600 = 0 |
tiene dos soluciones:
|
Para comprobar esta solución sustituimos los valores de x en la ecuación original.
| x2 - 50x + 600 = 0 |
| Para x = 30 se tiene: |
(30) 2 - 50 (30) +
600 = 0 900 - 1500 + 600 = 0 - 600 + 600 = 0 0 = 0 |
| Se cumple la igualdad. |
| Ahora, probemos para x = 20 |
(20) 2 - 50 (20) +
600 = 0 400 - 1000 + 600 = 0 - 600 + 600 = 0 0 = 0 |
| Se cumple la igualdad. |
Esto quiere decir que el valor de la "x" que está buscando Agapito puede ser 20 ó 30. Con estos valores se puede fácilmente obtener los valores de "y" que satisfacen sus ecuaciones.
| Cuando "x" vale 20: |
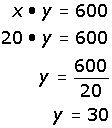 |
| Cuando "x" vale 30: |
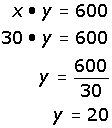 |
Si la "x" de su terreno vale 20, la "y" valdrá 30; y si la "x" vale 30, la "y" valdrá 20.
Por lo tanto el terreno de Agapito mide 20m por 30m.
FÓRMULA CUADRÁTICA
Aplicación de la formula cuadrática, para resolver ecuaciones de la forma ax2 + bx + c = 0.
Cuando una ecuación cuadrática no se pueda resolver fácilmente por factorización conviene utilizar la siguiente fórmula.
Para utilizar esta fórmula primero escriba la ecuación cuadrática en la forma ax2 + bx + c = 0.
El valor de a es el coeficiente del término cuadrático (x2).
El valor de b es el coeficiente de término "x" y "c" es la constante.
Finalmente, para encontrar los dos valores de "x" (la solución de la ecuación cuadrática) substituya en la fórmula los valores de a, b y c.
Ahora utilizando la fórmula cuadrática trataremos de resolver la ecuación cuadrática del problema de Agapito.
Recuerde que Agapito planteó su problema con dos ecuaciones de la siguiente manera:
| x • y = 600-----(1) x + y = 50-----(2) |
luego para resolver utilizó el método de ecuaciones simultaneas. Primero despejó la "y" de la segunda ecuación
| y = 50 - x |
y luego la sustituyó en la primera ecuación
| x (50-x) = 600 50x - x2 = 600 |
reordenando sus términos esta ecuación se puede expresar en forma estandar (ax2 + bx + c = 0) asi:
| -x2 + 50x - 600 = 0 |
Para aplicar la fórmula cuadrática.
|
|
determinamos los valores de a, b y c
| a = -1 por ser el coeficiente de x2 b = 50 por ser el coeficiente de x c = -600 por ser el valor de la constante |
sustituyendo a, b y c por sus valores se tiene:
|
x1 = 30 ; x2 = 20 |
 Por
lo que uno de los lados del terreno de Agapito puede medir 30
metros ó 20 metros, lo que
coincide con lo que se había obtenido antes.
Por
lo que uno de los lados del terreno de Agapito puede medir 30
metros ó 20 metros, lo que
coincide con lo que se había obtenido antes.
|
|
Para resolver ecuaciones cuadráticas o de segundo grado se recomienda aplicar directamente la fórmula:
|
Si desea saber cómo se desarrolla la fórmula cuadrática entre aquí:
Rolando tiene un terreno, en una esquina, con área de 500 m2. Cuando urbanizan tiene que poner una banqueta de 2 metros en dos lados como se muestra en el dibujo y le quedan sólo 414 m2. ¿Cuánto medía en cada lado el terreno? y ¿cuánto quedó midiendo en cada lado?
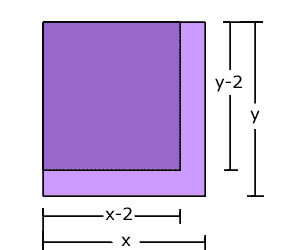
El terreno original tenía un área de 500 m2.
| x • y = 500 ------------ (1) |
El nuevo terreno, al quitarle 2 m en cada lado, queda con un área de 414 m2.
| (x - 2) (y - 2) = 414 ----
(2) |
Rolando despeja la "x" de la ecuación (1):
| |
y sustituye esta ecuación en la (2):
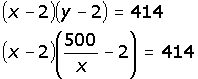 |

Se multiplican los binomios:
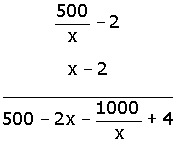 |
Con lo que la ecuación adquiere esta forma:
| |
simplificando
| |
multiplicando ambos términos por x y ordenando los exponentes del mayor al menor, se tiene lo siguiente:
| - 2x2 + 90x - 1,000 = 0 |
Se divide a toda la ecuación entre 2 para que el término cuadrático se vuelva unitario:
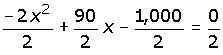 |
| - x2 + 45x - 500 = 0 |
Resuelve la ecuación aplicando la fórmula general para solución de ecuaciones de segundo grado:
 |
| Donde |
|
Sustituyendo los valor de a, b y c: |
|

Por lo anterior, Rolando sabe que uno de los lados de su terreno puede tener 20 m ó 25 m y como a cada lado le quitó 2 m para la banqueta quedó con lados de 18 ó 23 m.
El valor del otro lado se calcula sustituyendo el valor de x en la ecuación (1)
| |
| y1= 25
y2 =20 |