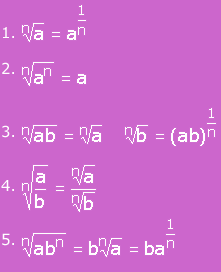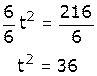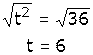Radicales
Si suponemos que an = k. En an el exponente "n"
indica el número de veces que se debe multiplicar a la cantidad
"a" por sí misma. En el radical 
el índice "n" indica el número de veces por el
que se multiplicó por sí mismo a un número (la base)
para diera la cantidad "k" . Por lo tanto
= a.
La raíz "n" de "k" es igual al número (la base) que elevado a la "n" potencia es igual a "k".
Observe que la radicación es la operación inversa de la potenciación.
Como sabemos que 62 = 36, se puede escribir lo siguiente:
Así mismo, como sabemos que 23 = 2 · 2 · 2 = 8 entonces la raíz cúbica de 8 se puede expresar así:
 |
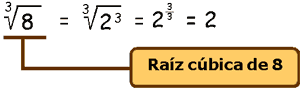
Observe que cuando el índice del radical es dos, no se escribe, pero se sabe que se trata de una raíz cuadrada. |
Cuando los índices de los radicales son números pares (2, 4, 6, 8, etcétera), la cantidad que va dentro del radical debe ser positiva, de otra manera la raíz no tendría solución.
Ejemplo
No tiene solución porque no hay números reales que su cuadrado dé -4.
Esto no sucede cuando se tiene un radical con un índice non (3, 5, 7, 9, etcétera).
Otra forma de escribir los radicales es la siguiente:
Ejemplos
 |
 |
|
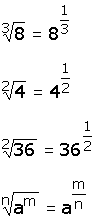Propiedades
de los radicales
|
Ejemplos
 |
 |
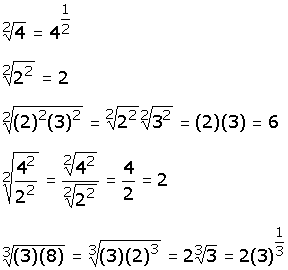Los radicales se utilizan para despejar algunas cantidades que tienen exponentes.
Ejemplo
Si se sabe que x2 = 4, ¿cuánto vale "x"?
En este caso, para despejar a la "x", se debe sacar raíz cuadrada en ambos miembros:
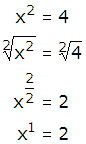
Ejemplo
¿Cuál será el valor de "t" si se tiene que 6 (t2) = 216?
Se despeja la "t" dividiendo ambos miembros entre 6:
|
Se despeja a la "t" sacando raíz cuadrada a ambos miembros:
|
Ejemplo
Si
la superficie o área de un círculo es de 28.26 m2,
¿cuál será su radio?
Se sabe que la superficie de un círculo se obtiene por medio de la fórmula:
|
Recuerde que  |
Se deberá despejar la "r", por lo que se hace lo siguiente.
Como la r2 está
multiplicada por 
,
se deben dividir los dos término entre .
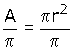
Como 
se tiene que:
Para dejar sola a la "r", es necesario sacar la raíz cuadrada de ambos miembros.
 |
|
||
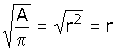
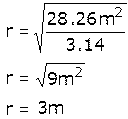Por lo que el radio será de 3 m.
Ejemplo
Si se tiene un tinaco en forma de cubo que tiene 1.728 m3 de volumen, ¿cuánto mide en cada lado ese tinaco?
Se sabe que para obtener el volumen de un cubo se puede utilizar la fórmula:
V = L3
|
Recuerde que
L es un lado del cubo |
Por lo que se deberá despejar o dejar sola a la "L", para lo que se debe sacar raíz cúbica en ambos miembros de la ecuación.
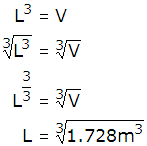
Se debe obtener un número que multiplicado por sí mismo tres veces dé 1.728 m3.
Esto se puede hacer por medio de tanteos, probando con varios números, o por medio de una calculadora que tenga la función de raíz cúbica.
Resolviendo la raíz cúbica
por
tanteos se tiene:
1.1 x 1.1 x 1.1=1.331 |
(falta para 1.728) |
1.3 x 1.3 x 1.3=2.197 |
(se pasó) |
1.2 x 1.2 x 1.2=1.798 |
(éste es el número) |
Por lo tanto, se tiene que:
Analizando las unidades que se tienen en este problema, se tiene lo siguiente:
El volumen está en m3 y cuando se saca la raíz cúbica se tiene:
Por lo que las unidades que se obtendrán serán metros; es decir, cada lado del tinaco mide 1.2 m.
Presione el siguiente botón y realice la actividad que se propone.
 |
||
 |
 |
 |