Unidad 4. Noticias de interés Tema 19. Cálculo de la probabilidad de eventos simples
| 19. ¡Buena suerte! |
Propósito: Calcularás la probabilidad de un evento simple relacionado con juegos.
 |
¿Compras billetes de la lotería con cierta frecuencia? ¿Alguna vez has ganado un premio en un juego de azar? |
En los juegos de azar se utilizan fichas, cartas o bolas, de igual tamaño y color para garantizar que cualquiera de ellas tenga igual probabilidad de salir o "caer". Por ejemplo, al lanzar una moneda al aire, la probabilidad de que "caiga" águila debe
| ser |  |
y de que "caiga" sol, | |
; si la moneda no está "cargada". |
| 1. |
Analiza los argumentos que dan Teresa, Rosalía y Francisca; después, realiza lo que se pide. |
|---|
|
| A) | ¿Quién de ellas tiene razón? ¿Por qué? |
|---|
| B) | El premio mayor es único, ¿qué probabilidad tiene cada una de ellas de que su número obtenga el premio mayor? |
|---|
Teresa, ; Rosalía, ;
Francisca,
| C) | El premio mayor es de $6 000 000. En caso que saliera premiado uno de esos números, ¿qué cantidad del premio le tocaría a la ganadora si sólo compró un "cachito", un vigésimo quinto de tres series? |
|---|
| D) | El impuesto por premios y sorteos es de 15 %. Finalmente, ¿qué cantidad de dinero recibiría? |
|---|
| E) | En ese sorteo había 5 premios de $2 000 000, ¿qué probabilidad tienen de que su número obtenga uno de estos premios? |
|---|
| F) | ¿La probabilidad es igual para las tres? ¿Por qué? |
|---|
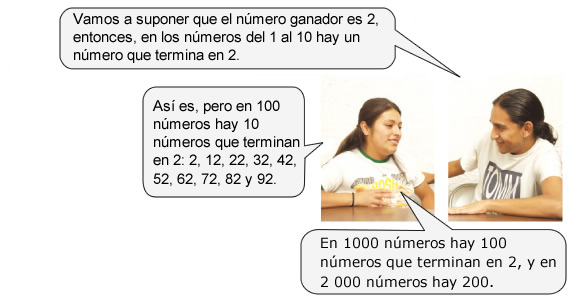
| G) | En la lotería, todos los billetes que no son premiados y terminan en la misma cifra que el número del premio mayor reciben reintegro, ¿cuál es la probabilidad de que al comprar un billete tenga reintegro? |
|---|
Analiza la forma en que Elvira y Jaime resuelven una situación similar.
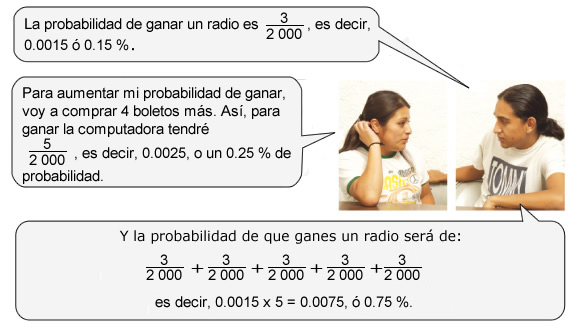
Para conseguir fondos, una escuela está rifando una computadora con lo último en tecnología. Para ello, están vendiendo 2000 boletos, del 0001 al 2000. Elvira compró el número 1111 y Jaime, el 0089.
|
Además de la computadora, van a rifar tres radios de bolsillo, ¿qué probabilidad tiene cada uno de ellos de ganar un radio?
Todos los boletos que terminen en la misma cifra que el número ganador tendrán derecho a una pluma. ¿Cuántas plumas tendrán que regalar?
|
| Resolvamos otros problemas |
| 2. |
En la rifa por televisión "Llame y gane una pantalla gigante", recibieron 5 000 llamadas. Emigdio hizo 2 llamadas. |
|---|
| A) | ¿Qué probabilidad tiene de ganar la pantalla? |
|---|
| B) | Su esposa Lupe hizo 15 llamadas, ¿quién tiene mayor probabilidad de ganar el premio? ¿Por qué? |
|---|
| C) | ¿Cuántas llamadas tendría que haber hecho para tener 1 % de probabilidad? |
|---|
| 3) |
Para el "Día de las madres", la estación televisora decidió que en su rifa "Llame y gane una pantalla gigante" iban a dar 20 boletos por cada llamada, e igualmente iban a recibir 5000 llamadas. Emigdio nuevamente hizo 2 llamadas.
|
|---|
| A) | ¿Qué probabilidad tiene de ganar la pantalla? |
|---|
| B) | ¿Aumentó la probabilidad de ganar con las nuevas condiciones? ¿Por qué? |
|---|
| C) | Su esposa Lupe pensó que no necesitaba hacer 15 llamadas, que con una llamada rebasaba el número de oportunidades que en la rifa anterior. ¿Es cierto lo que piensa? ¿Por qué? |
|---|
Observa el razonamiento de Cristina y Paco ante una situación similar. En la promoción de la nueva rifa por televisión "Llévese un guardarropa", van a dar 30 boletos por cada llamada, y reciben 6 000 llamadas.
 |
|||||
|
