Unidad 4. Noticias de interés Tema 18. Tratamiento frecuencial de la probabilidad
| 18. ¡Cuidado! |
Propósito: Conocerás el tratamiento frecuencial de la probabilidad.
 |
¿Sabías que el secuestro es un delito mediante el cual se priva de la libertad a una persona en contra de su voluntad con la finalidad de obtener dinero? |
Hace algunos años, las víctimas del secuestro eran empresarios, gente de negocios con una buena posición económica. Actualmente, también son profesionistas, obreros, campesinos, comerciantes, jóvenes y niños.
| 1. |
Analiza la siguiente información. |
|---|
La siguiente tabla muestra un estudio realizado con 540 casos de denuncias de secuestro.
|
| A) | ¿Cuando una banda de secuestradores elige a su víctima, ¿siempre logra su objetivo? |
|---|
| B) | ¿La probabilidad de que se lleve a cabo el secuestro es alta? |
|---|
| C) | ¿Hay más probabilidad de que se lleve acabo el secuestro o de que no? |
|---|
| D) | ¿Conoces alguna manera de calcular la probabilidad de que suceda algo? |
|---|
| 2. |
Pon en una bolsa oscura las 28 fichas de un dominó. |
|---|
Saca una ficha y escribe una raya (/) en la siguiente tabla, según sea la ficha que salga. Vuelve a poner la ficha en la bolsa y repite 100 veces.
|
|
Con base en la información de la tabla, realiza lo que se te pide.
| A) | ¿Cuántas veces la ficha que salió fue "mula" blanca? |
|---|
¿De 1?
¿De 2?
¿De 3?
¿De 4?
¿De 5?
¿De 6?
| B) | En total, ¿cuántas veces la ficha que salió fue "mula"? |
|---|
| C) | ¿Cuántas veces no fue "mula"? |
|---|
| D) | Escribe como razón el número de veces que salió "mula" entre el número total de veces que sacó fichas. |
|---|
Realiza la división
¿Obtuviste un número decimal menor que uno?
| E) | Escribe como razón el número de veces que salió una ficha que no es "mula" entre el número total de veces que sacó fichas. |
|---|
Realiza la división
¿Obtuviste un número decimal menor que uno?
| F) | ¿Cuánto suman ambas razones? ¿Por qué? |
|---|
|
La probabilidad estudia fenómenos aleatorios, es decir, donde pueden ocurrir varias cosas. Por ejemplo, de que al aventar un dado "caiga" 1, 2, 3, 4, 5 ó 6. La probabilidad indica la posibilidad de que ocurra un evento o hecho. Por ejemplo: qué probabilidad hay de que al lanzar un dado La idea básica es: Si un hecho se repite varias veces en condiciones idénticas, entonces la frecuencia relativa se obtiene al dividir el número de veces que aparece un resultado entre el total de las observaciones.
Ejemplo: Si al aventar un dado 30 veces, "cae" 4 veces 5, se puede decir que:
Por lo que la probabilidad de que "caiga" 5 es de dos quinceavos o de 0.133. |
| 3. |
Saca de la bolsa oscura todas las fichas que sean "mulas" y contesta las siguientes preguntas. |
|---|
| A) | ¿Cuál es la probabilidad de que al sacar una ficha de la bolsa sea "mula"? |
|---|
| B) | ¿Cuál es la probabilidad de que al sacar una ficha no sea "mula"?
|
|---|
| 4. |
Agrega a las 21 fichas que tienes en la bolsa una ficha que sea "mula". |
|---|
Saca una ficha y escribe una raya (/) en la tabla, según sea la ficha que salga. Vuelve a poner la ficha en la bolsa y repite 100 veces este procedimiento.
|
||||||||
Con base en la información de la tabla, realiza lo que se te pide.
| A) | ¿Cuántas veces la ficha que salió fue "mula"?
|
|---|
| B) | ¿Cuántas veces no lo fue?
|
|---|
| C) | Escribe como razón el número de veces que salió "mula" entre el número total de veces que sacaste una ficha. |
|---|
Realiza la división
¿Obtuviste un número decimal menor que uno?
| D) | Escribe como razón el número de veces que no salió "mula" entre el número total de veces que sacaste una ficha. |
|---|---|
Realiza la división
| E) | ¿Cuánto suman ambas razones? ¿Por qué? |
|---|---|
| F) | Si agregas una "mula" más a la bolsa, ¿aumenta la probabilidad de que al sacar una ficha sea "mula"? ¿Por qué? |
|---|---|
| G) | Si metes todas las fichas del dominó en la bolsa, ¿aumenta la probabilidad de que al sacar una ficha sea "mula"? ¿Por qué? |
|---|
 |
| 5. |
En el estudio sobre el secuestro, registraron lo siguiente: |
|---|
|
| A) | ¿Cuál es la probabilidad de salir con vida de un secuestro? |
|---|
| B) | ¿Cuál es la probabilidad de morir en un secuestro? |
|---|
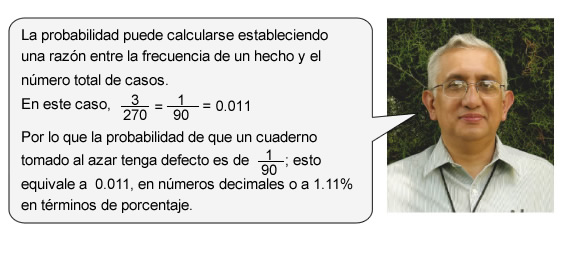
| 6. |
Analiza la siguiente nota informativa.
|
|---|
¡Es bueno saberlo! Un importante periódico de circulación nacional dio a conocer cifras que uno debe tener en cuenta en caso de ser víctima de secuestro.
Fuente:
Periódico Reforma, 4 de marzo de 2005, |
| A) | ¿Cuál es la probabilidad de que los secuestradores vean satisfechas sus demandas? |
|---|
| B) | ¿Qué probabilidad hay de que el secuestro sea cerca de la casa? |
|---|
| 7. |
Fernando quiere vender una carga de 3 000 huevos, donde hay 600 huevos descompuestos. ¿Cuál es la probabilidad de que el comprador al tomar un huevo al azar encuentre un huevo descompuesto?
|
|---|
| A) | Cociente: |
|---|
| B) | Decimal: |
|---|
| C) | Porcentaje: |
|---|
| 8. | Un estudio demostró que de 850 compras que se realizaron a través de internet, 34 tuvieron alguna irregularidad. ¿Cuál es la probabilidad de que al realizar una compra a través de internet haya alguna irregularidad? Simplifica la fracción. |
|---|
| A) | Cociente: |
|---|
=
| B) | Decimal: |
|---|
| C) | Porcentaje: |
|---|
| 9. | Lee con mucha atención la siguiente noticia periodística y contesta las preguntas que se hacen. |
|---|
Reconocen alto riesgo en el trabajo
Fuente: Periódico El Universal, 24 de abril de 2005. p. A 13. |
| A) | En los últimos años, ¿ha aumentado o disminuido la probabilidad de sufrir un accidente de trabajo? |
|---|
| B) | En México, ¿cuál es la probabilidad de que un accidente de trabajo termine en fallecimiento? |
|---|
| C) | En México, ¿cuál es la probabilidad de sufrir un accidente de trabajo? |
|---|
| D) | En nuestro país, ¿en cuáles actividades se tiene un mayor riesgo de morir? |
|---|
|
 |
