LECTURA 2.2 - El movimiento con aceleración uniforme

El movimiento con aceleración uniforme.

Los movimientos acelerados más fáciles de describir son los que siguen una trayectoria rectilínea y en los que la magnitud de la velocidad aumenta o disminuye en forma constante.

Un ejemplo de este tipo de movimiento se presenta cuando un corredor inicia su carrera partiendo del reposo (v₁ = 0 m/s) e incrementa su velocidad en 2 m/s cada segundo. Aquí su aceleración es constante e igual a 2 m/s². En la siguiente tabla se muestra la velocidad que adquiere como función del tiempo.

Tiempo (s)	0	1	2	3	4	5
Velocidad (m/s)	0	2	4	6	8	10

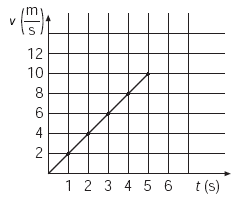
Si se construye una gráfica velocidad-tiempo con esta información, se obtiene:

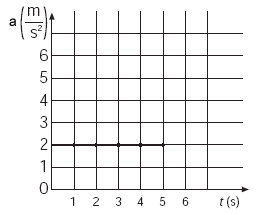
La gráfica muestra que la velocidad no es constante, pero aumenta uniformemente con el tiempo. El incremento de velocidad es directamente proporcional al intervalo de tiempo que transcurre y por eso se obtiene una línea recta inclinada.

La aceleración del corredor es constante, por lo cual la gráfica de la aceleración como función del tiempo (gráfica aceleración-tiempo) es una recta horizontal que indica que la aceleración no cambia.

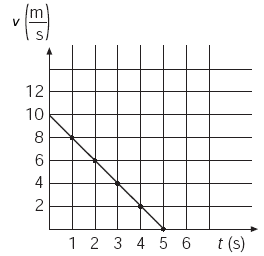
Este tipo de movimiento recibe el nombre de movimiento uniformemente acelerado y en él la magnitud de la velocidad aumenta o disminuye de manera uniforme con el tiempo. Así, si el corredor del ejemplo decidiera detenerse disminuyendo su velocidad con una aceleración constante de – 2 m/s², su movimiento también sería uniformemente acelerado y se representaría como se muestra en la gráfica siguiente.

Si se conoce la aceleración media de un objeto, puede predecirse cuánto cambiará su velocidad en un cierto intervalo de tiempo: basta multiplicar la aceleración por el tiempo transcurrido.

Esto es así porque la aceleración es una medida de cambio de velocidad por unidad de tiempo. Si el objeto ya tenía una velocidad inicial (v_i), su velocidad final (v_f), al cabo de un tiempo Ðt, se obtiene sumando el incremento (o la reducción) Δv al valor inicial.

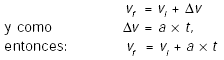Cuando la aceleración es cero, no se produce ningún cambio en la velocidad y su valor final es igual al inicial: el movimiento es a velocidad constante.

En la vida cotidiana, es común confundir la aceleración de un objeto con su velocidad. A veces se cree que si un objeto tiene una gran aceleración significa que “va muy rápido”. Esto no es así; un objeto puede tener una velocidad muy grande y una aceleración igual a cero: su velocidad es grande, pero constante.

En el movimiento uniformemente acelerado, la velocidad crece o disminuye proporcionalmente con el tiempo; pero, ¿qué pasa con el desplazamiento del objeto?, ¿cómo varía su posición con el tiempo? Para responder a estas preguntas, conviene recordar lo que sucede en el movimiento rectilíneo uniforme.

Si un nadador, por ejemplo, se mueve a velocidad constante, la gráfica velocidad-tiempo que le corresponde es una línea horizontal que indica que la velocidad no cambia. En este caso, el desplazamiento que realiza el cuerpo en un tiempo t se obtiene como:

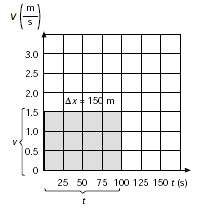
Este producto corresponde al área del rectángulo de la gráfica, cuya base es igual al tiempo transcurrido (t) y su altura es la velocidad constante v.

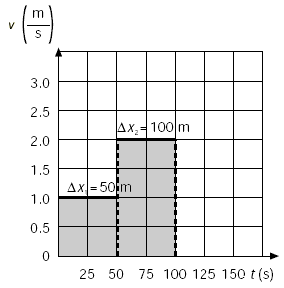
Si el mismo nadador se moviera a cierta velocidad constante durante la mitad del tiempo y después incrementara bruscamente su valor para mantenerlo así el resto del tiempo, la gráfica sería como la que se ilustra a continuación. En este caso, el desplazamiento en el primer intervalo de tiempo estaría dado por el área bajo la primera recta y el área del segundo rectángulo indicaría la magnitud del desplazamiento posterior.

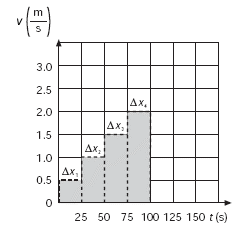
Como el nadador se mueve a mayor velocidad en la segunda parte de su movimiento, su desplazamiento es mayor que el realizado en el primer intervalo de tiempo. La suma de los dos desplazamientos es igual al desplazamiento total
(ΔX_f = ΔX₁ + ΔX₂ = 150 m en la gráfica).

Si el nadador incrementara su velocidad en cuatro etapas diferentes, manteniendo en cada una su velocidad constante, el desplazamiento en cada etapa estaría dado por el área de los rectángulos de la siguiente figura.

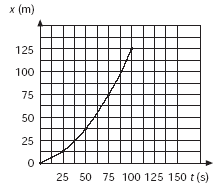
La posición del nadador al inicio de cada etapa podría obtenerse al sumar las áreas en las etapas anteriores. Así, si parte de x = 0 y se desplaza 12.5 m en los primeros 25 s, pasará a x = 12.5 m; en el siguiente intervalo de tiempo se desplaza 25 m y su nueva posición será x = 12.5 + 25 = 37.5, etc. La gráfica posición-tiempo para este movimiento mostraría cómo el nadador cada vez se desplaza más en un mismo tiempo, como se indica a continuación:

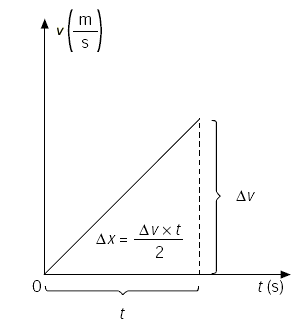
En el movimiento uniformemente acelerado el desplazamiento total también puede obtenerse calculando el área bajo la gráfica velocidad-tiempo. En este caso, la gráfica es una línea recta inclinada y, si el móvil parte del reposo (v_i = 0), el área que se busca corresponde a la de un triángulo cuya base es el tiempo t y la altura es igual al cambio de velocidad Δv (Fig. 1). El desplazamiento Ðx resulta:

Como en este tipo de movimiento Δv = a x t

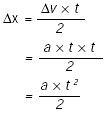De acuerdo con esta relación, un objeto con una aceleración de 2 m/s², por ejemplo, en 5 s se desplazará 2 x (5)²/2 = 25 m; en un intervalo de 10 s se desplazará 2 x (10)²/2 = 100 m y a los 15 s alcanzarán los 2 x(15)²/2 = 225 m.

Fig. 1 Cálculo del desplazamiento en un movimiento uniformemente acelerado.

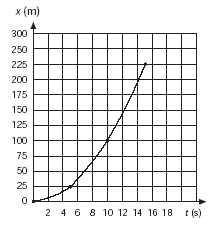
Si el cuerpo parte del origen, estos desplazamientos señalan la posición que alcanza después de cierto tiempo, y al hacer la gráfica posición-tiempo se obtiene una curva (Fig. 2). La gráfica muestra que el cambio en la posición del objeto es cada vez mayor para el mismo intervalo de tiempo; esto sucede porque la velocidad se incrementa constantemente.

Fig. 2 Gráfica posición-tiempo en un movimiento uniformemente acelerado.